已知函数f(x)=sin(ωx+?)(ω>0,0<?<π)的图象与直线y=b(-1<b<0)的三个相邻交点的横坐标分别是1,2,4.
(1)求f(x)的解析式,并写出f(x)的单调递减区间;
(2)设g(x)=f(2x)+f(x),求函数g(x)的值域.
解:(1)依题意得,周期T=4-1=3,所以
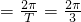
,
由对称性知,当
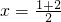
=

时,函数取得最小值-1,
∴
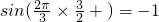
所以
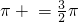
,
所以
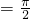
,所以
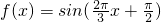
.
∵y=sinx的单调减区间是[2kπ+

,2kπ+

]
∴
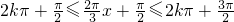
∴
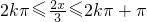
∴
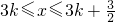
所以函数f(x)的单调减区间是
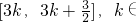
Z.
(2)由(1)知
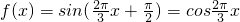
,
所以
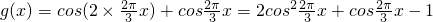
,
令
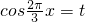
,则根据余弦函数的值域得到t∈[-1,1],
所以
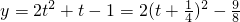
,
当t=-

时,函数取得最小值-

,当t=1时,函数取得最大值2,
所以g(x)的值域为
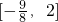
.
分析:(1)根据函数的图象与横轴的三个交点,做出函数的解析式,根据函数的对称性看出函数的一个点的坐标,代入函数的解析式,求出初相的值,写出函数的解析式,根据正弦函数的解析式写出函数的单调区间.
(2)根据上一问做出的函数的解析式,写出函数g(x)的解析式,对三角函数式进行化简整理,得到关于余弦的二次函数,根据二次函数的最值的求法得到结果.
点评:本题考查三角函数的解析式和有关性质,本题解题的关键是正确求出函数的解析式,再进行后面的单调区间和值域的求法,这种题目是高考卷中每一年都要出现,注意题目的开始解析式不要出错,本题是一个中档题目.

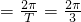 ,
,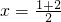 =
= 时,函数取得最小值-1,
时,函数取得最小值-1,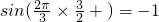
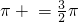 ,
,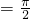 ,所以
,所以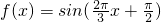 .
. ,2kπ+
,2kπ+ ]
]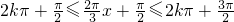
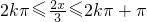
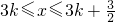
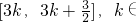 Z.
Z.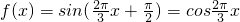 ,
,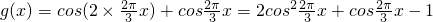 ,
,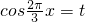 ,则根据余弦函数的值域得到t∈[-1,1],
,则根据余弦函数的值域得到t∈[-1,1],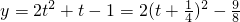 ,
, 时,函数取得最小值-
时,函数取得最小值- ,当t=1时,函数取得最大值2,
,当t=1时,函数取得最大值2,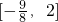 .
.

