
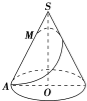
 如图所示,已知在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求绳子最短时,顶点到绳子的最短距离$\frac{4x}{\sqrt{{x}^{2}+16}}$(用x表示).
如图所示,已知在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求绳子最短时,顶点到绳子的最短距离$\frac{4x}{\sqrt{{x}^{2}+16}}$(用x表示). 分析 算出侧面展开扇形圆心角α=90°,因此将圆锥侧面展开,可得绳子的最短长度为Rt△ASM中斜边AM的长,由此利用勾股定理即可算出f(x)的表达式;由平面几何性质,可得绳子最短时定点S到绳子的最短距离等于Rt△ASM的斜边上的高,利用三角形面积等积变换求解,可得这个最短距离的表达式.
解答 解:∵底面半径r=1,母线长l=4,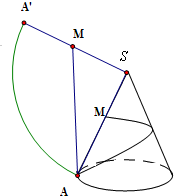
∴侧面展开扇形的圆心角α=90°
因此,将圆锥侧面展开成一个扇形,从点M拉一绳子围绕圆锥侧面转到点A,最短距离为Rt△ASM中,斜边AM的长度
∵SM=x,SA=4
∴绳子的最短长度的平方f(x)=AM2=x2+42=x2+16.
绳子最短时,定点S到绳子的最短距离等于Rt△ASM的斜边上的高,设这个距离等于d,
则d=$\frac{SM•AS}{AM}$=$\frac{4x}{\sqrt{{x}^{2}+16}}$,
故答案为$\frac{4x}{\sqrt{{x}^{2}+16}}$.
点评 本题在圆锥的表面拉一根绳子,求绳子长度的最小值.着重考查了圆锥的侧面展开、勾股定理与三角形面积公式等知识,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | $\frac{{2\sqrt{2}}}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | (¬p)∨(¬q) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com