
分析 由已知可求出g(x)的解析式,分类讨论出函数在各段上的单调性,进而求出函数的最值的表达式,进而可得p(a)的表达式,进而可求出p(a)的最小值.
解答 解:∵f(x)=$\left\{{\begin{array}{l}{1,(1≤x≤2)}\\{x-1,(2<x≤3)}\end{array}}$对于实数a将g(x)=f(x)-ax,
∴g(x)=$\left\{\begin{array}{l}{1-ax,1≤x≤2}\\{(1-a)x-1,2<x≤3}\end{array}\right.$
当1≤x≤2时,g(x)max=1-a,g(x)min=1-2a,
当2≤x≤3时,若0≤a≤1,则g(x)在[2,3]上递增,
g(x)max=2-3a,g(x)min=1-2a,
当a>1时,则g(x)在[2,3]上递减,
g(x)max=1-2a,g(x)min=2-3a,
∴0<a≤$\frac{1}{2}$,g(x)max=2-3a,g(x)min=1-2a
当$\frac{1}{2}$<a≤1,g(x)max=1-a,g(x)min=2-3a
当a>1时,g(x)max=1-a,g(x)min=2-3a,
当a≤0时,g(x)max=2-3a,g(x)min=1-2a
∴$p(a)=\left\{{\begin{array}{l}{1-2a,(a≤0)}\\{1-a,(0<a≤\frac{1}{2})}\\{a,(\frac{1}{2}<a≤1)}\\{2a-1,(a>1)}\end{array}}\right.$
当a=$\frac{1}{2}$时最小值为$\frac{1}{2}$
点评 本题考查的知识点是函数的最值及其几何意义,分段函数,其中分段函数分段处理是解答此类问题的常用方法.


科目:高中数学 来源: 题型:填空题
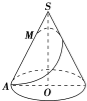 如图所示,已知在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求绳子最短时,顶点到绳子的最短距离$\frac{4x}{\sqrt{{x}^{2}+16}}$(用x表示).
如图所示,已知在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求绳子最短时,顶点到绳子的最短距离$\frac{4x}{\sqrt{{x}^{2}+16}}$(用x表示).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3≤x<-1或1<x≤2} | B. | {x|-3<x≤-1或1<x<2} | C. | {x|-3≤x≤-1或1≤x<2} | D. | {x|-3≤x≤-1或1<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
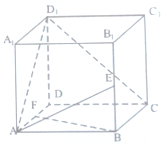 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方体,E,F分别是棱B1B,DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方体,E,F分别是棱B1B,DA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x0∈R,使得x02-1<0”的否定是“?x∈R,均有x2-1>0” | |
| B. | 命题“存在四边相等的空间四边形不是正方形”,该命题是假命题 | |
| C. | 命题“若x2=y2,则x=y”的逆否命题是真命题 | |
| D. | 命题“若x=3,则x2-2x-3=0”的否命题是“若x≠3,则x2-2x-3≠0” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com