
科目:高中数学 来源:不详 题型:解答题
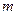 人,每人每年可创利100千元.据测算,若裁员人数不超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利1千元;若裁员人数超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利2千元.为保证公司的正常运转,留岗的员工数不得少于现有员工人数的75%.为保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.
人,每人每年可创利100千元.据测算,若裁员人数不超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利1千元;若裁员人数超过现有人数的20%,则每裁员1人,留岗员工每人每年就能多创利2千元.为保证公司的正常运转,留岗的员工数不得少于现有员工人数的75%.为保障被裁员工的生活,公司要付给被裁员工每人每年20千元的生活费.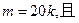 15<
15<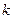 <50,为了获得最大的经济效益,该公司应裁员多少人?
<50,为了获得最大的经济效益,该公司应裁员多少人?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x |
| x2+x+1 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(1,2,3,4) | B.(0,3,4,0) | C.(-1,0,2,-2) | D.(0,-3,4,-1) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.[1,+∞) | B.(1,+∞) | C.(-∞,1] | D.(-∞,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com