
分析 (1)设A(2pt12,2pt1),B(2pt22,2pt2).由OA⊥OB,利用斜率计算公式可得kOA•kOB=-1,得出t1t2=-1.
又kAB=$\frac{1}{{t}_{1}+{t}_{2}}$,即可得出直线AB的方程,利用直线系即可得出.
(2)确定点H的轨迹是以OM为直径的圆(不含原点O),即可求点H的轨迹方程.
解答 (1)证明:设A(2pt12,2pt1),B(2pt22,2pt2).
由OA⊥OB,得$\frac{2p{t}_{1}}{2p{{t}_{1}}^{2}}$•$\frac{2p{t}_{2}}{2p{{t}_{2}}^{2}}$=-1,得出t1t2=-1.
∴kAB=$\frac{1}{{t}_{1}+{t}_{2}}$.
得直线AB的方程:y-2pt1=$\frac{1}{{t}_{1}+{t}_{2}}$(x-2pt12).
即x-(t1+t2)y-2p=0.
令y=0,解得x=2p.
∴直线AB恒过定点(2p,0).
(2)解:∵直线AB恒过定点M(2p,0),过原点O作0H垂直于AB,H为垂足,
∴点H的轨迹是以OM为直径的圆(不含原点O),
∴点H的轨迹方程为(x-p)2+y2=p2(x≠0).
点评 熟练掌握抛物线的性质、斜率计算公式、直线方程、直线系等是解题的关键.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{19}{10}$ | B. | $\frac{21}{40}$ | C. | $\frac{9}{20}$ | D. | $\frac{11}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2-n | C. | 21-n | D. | 2-2n |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北涞水波峰中学高一9月月考数学试卷(解析版) 题型:选择题
以下六个写法中:①{0}∈{0,1,2}; ②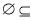 {1,2}; ③
{1,2}; ③ ④{0,1,2}={2,0,1}; ⑤
④{0,1,2}={2,0,1}; ⑤ ; ⑥
; ⑥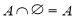 ,正确的个数有( )
,正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com