
分析 (1)根据函数的定义域和值域之间的关系进行计算即可.
(2)根据不等式关系使用插板法进行分组即可.
解答 解:(1)以集合A为定义域,B为值域的函数等价为将四个数1,2,3,4,分成两组,一组对应函数值5,一组对应函数值6,
则有${C}_{4}^{1}+{C}_{4}^{2}+{C}_{4}^{3}$=4+6+4=14种函数.
(2)若满足条件 f(1)≤f(2)≤f(3)≤f(4),
则等价为将1,2,3,4按照固定顺序分成两组,前面一组对应5,后面一组对应6,使用插板法,
1,2,3,4中间共有3个空,则共有${C}_{3}^{1}$=3种,分别为f(1)=5,f(2)=f(3)=f(4)=6或f(1)=f(2)=5,f(3)=f(4)=6,
或f(1)=f(2)=f(3)=5,f(4)=6.
点评 本题主要考查函数定义域和值域之间的关系,以及简单的计数问题,比较基础.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在△ABC中,D是BC边上的一点,且BD=2DC,用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示$\overrightarrow{AD}$.
如图所示,在△ABC中,D是BC边上的一点,且BD=2DC,用$\overrightarrow{AB}$、$\overrightarrow{AC}$表示$\overrightarrow{AD}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(0,1) | B. | (-∞,-1)∪(-1,0) | C. | (-1,0)∪(0,+∞) | D. | [-1,0)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2016-2017学年云南大理州南涧县民族中学高二文9月月考数学试卷(解析版) 题型:选择题
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f(-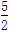 )等于( )
)等于( )
A.-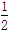 B.-
B.-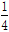 C.
C. 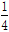 D.
D. 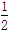
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com