
【题目】在菱形![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的中点(如图1).将
的中点(如图1).将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,
,![]() 为线段
为线段![]() 的中点(如图2).
的中点(如图2).
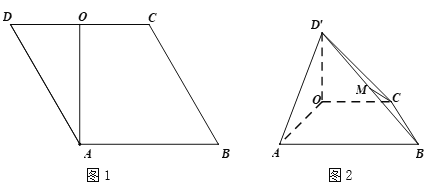
(Ⅰ)求证:![]() ;
;
(Ⅱ)求证:![]() 平面
平面![]() ;
;
(Ⅲ)当四棱锥![]() 的体积为
的体积为![]() 时,求
时,求![]() 的值.
的值.
【答案】(Ⅰ)见解析. (Ⅱ)见解析. (Ⅲ) ![]() .
.
【解析】
(Ⅰ)证明OD'⊥AO. 推出OD'⊥平面ABCO. 然后证明OD'⊥BC.(Ⅱ)取P为线段AD'的中点,连接OP,PM;证明四边形OCMP为平行四边形,然后证明CM∥平面AOD';(Ⅲ)说明OD'是四棱锥D'﹣ABCO的高.通过体积公式求解即可.
(Ⅰ)证明:因为在菱形![]() 中,
中,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,
所以![]() .
.
因为平面![]() 平面
平面![]()
平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,
,
所以![]() .
.
(Ⅱ)证明:如图,取![]() 为线段
为线段![]() 的中点,连接OP,PM;
的中点,连接OP,PM;
因为在![]() 中,
中,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点,
的中点,
所以![]() ,
,![]() .
.
因为![]() 是线段
是线段![]() 的中点,菱形
的中点,菱形![]() 中,
中,![]() ,
,![]() ,
,
所以![]() .
.
所以![]() ,
,![]() .
.
所以![]() ,
,![]() .
.
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
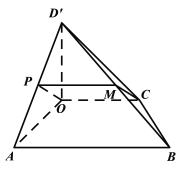
(Ⅲ)由(Ⅰ)知![]() 平面
平面![]() .
.
所以![]() 是四棱锥
是四棱锥![]() 的高,又S=
的高,又S=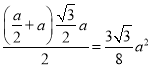 ,
,![]()
因为![]() ,
,
所以![]() .
.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】某蔬果经销商销售某种蔬果,售价为每公斤25元,成本为每公斤15元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价以每公斤10元处理完.根据以往的销售情况,得到如图所示的频率分布直方图:

(1)根据频率分布直方图计算该种蔬果日需求量的平均数![]() (同一组中的数据用该组区间中点值代表);
(同一组中的数据用该组区间中点值代表);
(2)该经销商某天购进了250公斤这种蔬果,假设当天的需求量为![]() 公斤
公斤![]() ,利润为
,利润为![]() 元.求
元.求![]() 关于
关于![]() 的函数关系式,并结合频率分布直方图估计利润
的函数关系式,并结合频率分布直方图估计利润![]() 不小于1750元的概率.
不小于1750元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数)曲线C2的参数方程为
为参数)曲线C2的参数方程为![]() (
(![]() ,
,![]() 为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=
为参数)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=![]() 与C1,C2各有一个交点.当
与C1,C2各有一个交点.当![]() =0时,这两个交点间的距离为2,当
=0时,这两个交点间的距离为2,当![]() =
=![]() 时,这两个交点重合.
时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值;
(2)设当![]() =
=![]() 时,l与C1,C2的交点分别为A1,B1,当
时,l与C1,C2的交点分别为A1,B1,当![]() =-
=-![]() 时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点为A2,B2,求四边形A1A2B2B1的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角三角形![]() 所在的平面与半圆弧
所在的平面与半圆弧![]() 所在平面相交于
所在平面相交于![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点, ![]() 是
是![]() 上异于
上异于![]() ,
,![]() 的点,
的点, ![]() .
.
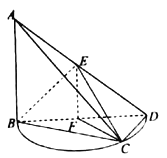
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若点![]() 为半圆弧
为半圆弧![]() 上的一个三等分点(靠近点
上的一个三等分点(靠近点![]() )求二面角
)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
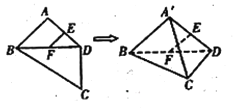
【题目】如图,平面四边形![]() 中,
中,![]() ,
,![]() 是
是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
A.![]() 平面
平面![]()
B.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
C.异面直线![]() 与
与![]() 所成的角为
所成的角为![]()
D.直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
设函数f(x)=alnx﹣bx2(x>0).
(1)若函数f(x)在x=1处于直线![]() 相切,求函数f(x)在
相切,求函数f(x)在![]() 上的最大值;
上的最大值;
(2)当b=0时,若不等式f(x)≥m+x对所有的a∈[1,![]() ],x∈[1,e2]都成立,求实数m的取值范围.
],x∈[1,e2]都成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M过两点A(1,﹣1),B(﹣1,1),且圆心M在x+y﹣2=0上,
(Ⅰ)求圆M的方程;
(Ⅱ)设P是直线x+y+2=0上的动点.PC,PD是圆M的两条切线,C,D为切点,求四边形PCMD面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com