
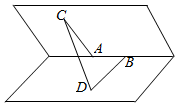
 如图,已知在一个二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2$\sqrt{17}$cm,则这个二面角的度数为60°.
如图,已知在一个二面角的棱上有两个点A、B,线段AC、BD分别在这个二面角的两个面内,并且都垂直于棱AB,AB=4cm,AC=6cm,BD=8cm,CD=2$\sqrt{17}$cm,则这个二面角的度数为60°. 分析 设这个二面角的度数为α,由题意得$\overrightarrow{CD}$=$\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,从而得到cosα=$\frac{1}{2}$,由此能求出结果.
解答 解:设这个二面角的度数为α,
由题意得$\overrightarrow{CD}$=$\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BD}$,
∴${\overrightarrow{CD}}^{2}$=${\overrightarrow{CA}}^{2}$+${\overrightarrow{AB}}^{2}$+${\overrightarrow{BD}}^{2}$+2|$\overrightarrow{CA}$|•|$\overrightarrow{BD}$|cos(π-α),
∴(2$\sqrt{17}$)2=36+16+64-2×6×8×cosα,
解得cosα=$\frac{1}{2}$,
∴α=60°.
∴这个二面角的度数为60°.
故答案为:60°.
点评 本题考查的知识要点:余弦定理的应用,勾股定理的应用,线面垂直的性质,二面角的应用.属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | B. | $\frac{1}{2}$$\overrightarrow{b}$+$\frac{1}{2}$$\overrightarrow{c}$ | C. | $\frac{1}{3}$$\overrightarrow{b}$+$\frac{2}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}$$\overrightarrow{b}$+$\frac{4}{3}$$\overrightarrow{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
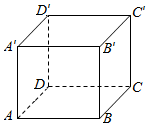
 如图在正方体ABCD-A1B1C1D1中,E,F,M,N分别为棱AD,AB,DC,BC的中点.
如图在正方体ABCD-A1B1C1D1中,E,F,M,N分别为棱AD,AB,DC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
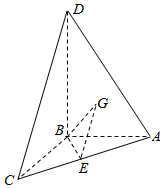 如图,四面体D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC的中点,G是△ABD的重心,异面直线AD与BE所成的角为θ,且$cosθ=\frac{{\sqrt{10}}}{10}$
如图,四面体D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC的中点,G是△ABD的重心,异面直线AD与BE所成的角为θ,且$cosθ=\frac{{\sqrt{10}}}{10}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
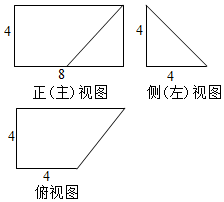 已知某几何体的三视图如图所示,则该几何体的体积等于( )
已知某几何体的三视图如图所示,则该几何体的体积等于( )| A. | $\frac{80}{3}$ | B. | 50 | C. | $\frac{160}{3}$ | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com