练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．在正方体ABCD-A1B1C1D1中，平面C1-AB-C所成的二面角的大小是（　　）
    A．30°B．45°C．60°D．90°

    分析 由C1B⊥AB，BC⊥AB，知∠C1BC是面C1-AB-C所成的二面角的平面角，由此能求出面C1-AB-C所成的二面角的大小．

    解答 解∵AB⊥平面BCC1B1，
    ∴C1B⊥AB，BC⊥AB，
    ∴∠C1BC是面C1-AB-C所成的二面角的平面角，
    ∵BC=CC1，且BC⊥CC1，
    ∴∠C1BC=45°．
    ∴面C1-AB-C所成的二面角的大小为45°．
    故选：B．

    点评 本题考查二面角的大小的求法，是基础题，解题时要认真审题，注意空间思维能力的培养．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    6．已知三棱锥S-ABC各顶点都在球O的球面上，若SA=SB=SC=1，且SA、SB、SC两两垂直，则球O的表面积为3π．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．某小卖部为了研究热茶销售量y（杯）与气温x（℃）之间的关系，随机统计了某4天热茶销售量与当天气温，并制作了对照表：
    气温°C1496-5
    茶销售量（杯）34444874
    由表中数据算得线性回归方程$\widehaty=bx+a$中b≈-2
    （1）求y对x的线性回归方程；
    （2）预测当气温为-1℃时，热茶销售量．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

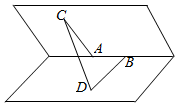    10．如图，已知在一个二面角的棱上有两个点A、B，线段AC、BD分别在这个二面角的两个面内，并且都垂直于棱AB，AB=4cm，AC=6cm，BD=8cm，CD=2$\sqrt{17}$cm，则这个二面角的度数为60°．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

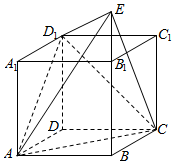    17．直四棱柱ABCD-A1B1C1D1中，底面ABCD为菱形，且∠BAD=60°，A1A=AB，E为BB1延长线上的一点，D1E⊥面D1AC．设AB=2．
    （Ⅰ）求二面角E-AC-D1的大小； 
    （Ⅱ）在D1E上是否存在一点P，使A1P∥面EAC？若存在，求D1P：PE的值；不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．在一个正方体ABCD-A1B1C1D1中，P为正方形A1B1C1D1四边上的动点，O为底面正方形ABCD的中心，M，N分别为AB，CD的中点，点Q为平面SKABCD内一点，线段D1Q与OP互相平分，则满足$\overrightarrow{MQ}$=λ$\overrightarrow{MN}$的实数λ的值有2个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

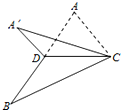    14．如图，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A1CD，所成二面角A1-CD-B的平面角为α，则（　　）
    A．∠A1CB≥αB．∠A1DB≤αC．∠A1DB≥αD．∠A1CB≤α

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

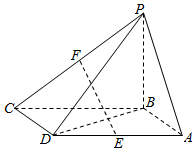    11．如图，四棱锥P-ABCD的底面ABCD是平行四边形，PB⊥面ABCD，BA=BD=$\sqrt{2}$，AD=2，E，F分别是棱AD，PC的中点．
    （1）证明：EF∥平面PAB；
    （2）若二面角P-AD-B为60°，求直线EF与平面PBC所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．若抛物线y=x2-6x+5与坐标轴的交点都在圆C上．
    （1）求圆C的方程；
    （2）若圆C与直线x-y+a=0交于A，B两点，且CA⊥CB，求a的值．

    查看答案和解析>>

    同步练习册答案