
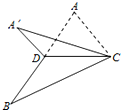
 如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A1CD,所成二面角A1-CD-B的平面角为α,则( )
如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A1CD,所成二面角A1-CD-B的平面角为α,则( )| A. | ∠A1CB≥α | B. | ∠A1DB≤α | C. | ∠A1DB≥α | D. | ∠A1CB≤α |
分析 设∠ADC=θ,AB=2,则由题意知AD=BD=A1D=1.在空间图形中,连结A1B,设A1B=t.推导出cos∠A1DB=$\frac{2-{t}^{2}}{2}$.过A1作A1N⊥DC,过B作BM⊥DC,垂足分别为N、M.过N作NP∥MB,使四边形BPNM为平行四边形,则NP⊥DC.连结A1P,BP,∠A1NP就是二面角A1-CD-B的平面角,∠A1NP=α.由此能推导出α≤∠A1DB.
解答 解:设∠ADC=θ,AB=2,则由题意知AD=BD=A1D=1.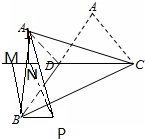
在空间图形中,连结A1B,设A1B=t.
在△A1DB中,cos∠A1DB=$\frac{{A}_{1}{D}^{2}+D{B}^{2}-{A}_{1}{B}^{2}}{2{A}_{1}D×DB}$=$\frac{{1}^{2}+{1}^{2}-{t}^{2}}{2×1×1}$=$\frac{2-{t}^{2}}{2}$.
过A1作A1N⊥DC,过B作BM⊥DC,垂足分别为N、M.
过N作NP∥MB,使四边形BPNM为平行四边形,则NP⊥DC.连结A1P,BP,
则∠A1NP就是二面角A1-CD-B的平面角,所以∠A1NP=α.
在Rt△A1ND中,DN=A1Dcos∠A1DC=cos θ,A1N=A1Dsin∠A1DC=sin θ.
同理,BM=PN=sin θ,DM=cos θ,故BP=MN=2cos θ.
由题意BP⊥平面A1NP,故BP⊥A1P.
在Rt△A1BP中,A1P2=A1B2-BP2=t2-(2cos θ)2=t2-4cos2θ.
在△A1NP中,cos α=cos∠A1NP=$\frac{{A}_{1}{N}^{2}+N{P}^{2}-{A}_{1}{P}^{2}}{2{A}_{1}N×NP}$
=$\frac{si{n}^{2}θ+si{n}^{2}θ-({t}^{2}-4co{s}^{2}θ)}{2sinθ×sinθ}$=$\frac{2+2co{s}^{2}θ-{t}^{2}}{2si{n}^{2}θ}$
=$\frac{2-{t}^{2}}{2si{n}^{2}θ}+\frac{co{s}^{2}θ}{si{n}^{2}θ}$=$\frac{1}{si{n}^{2}θ}cos∠{A}_{1}DB+\frac{co{s}^{2}θ}{si{n}^{2}θ}$.
∴cos α-cos∠A1DB=$\frac{1}{si{n}^{2}θ}$cos∠A1DB+$\frac{co{s}^{2}θ}{si{n}^{2}θ}$-cos∠A1DB
=$\frac{1-si{n}^{2}θ}{si{n}^{2}θ}$cos∠A1DB+$\frac{co{s}^{2}θ}{si{n}^{2}θ}$
=$\frac{co{s}^{2}θ}{si{n}^{2}θ}$(1+cos∠A1DB)≥0,
∴cos α≥cos∠A1DB(当θ=$\frac{π}{2}$时取等号),
∵α,∠A1DB∈[0,π],而y=cos x在[0,π]上为递减函数,
∴α≤∠A1DB.
故选:C.
点评 本题主要考查空间中的立体几何,考查考生的空间想象能力及分析问题、解决问题的能力.本题可采用特殊位置法进行排除.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图在正方体ABCD-A1B1C1D1中,E,F,M,N分别为棱AD,AB,DC,BC的中点.
如图在正方体ABCD-A1B1C1D1中,E,F,M,N分别为棱AD,AB,DC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
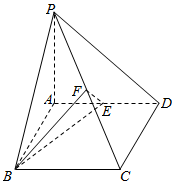 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2$\sqrt{2}$,E,F分别是AD,PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB=2,BC=2$\sqrt{2}$,E,F分别是AD,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
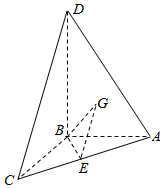 如图,四面体D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC的中点,G是△ABD的重心,异面直线AD与BE所成的角为θ,且$cosθ=\frac{{\sqrt{10}}}{10}$
如图,四面体D-ABC中,AB,BC,BD两两垂直,且AB=BC=2,点E是AC的中点,G是△ABD的重心,异面直线AD与BE所成的角为θ,且$cosθ=\frac{{\sqrt{10}}}{10}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 一个几何体的三视图如图,则该几何体的表面积为( )
一个几何体的三视图如图,则该几何体的表面积为( )| A. | 8+6$\sqrt{2}$ | B. | 10+8$\sqrt{2}$ | C. | 12+4$\sqrt{2}$ | D. | 14+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com