
分析 由a1=1,an+1-an∈{a1,a2,…,an}(n∈N+),分别令n=2,3,4,5,求得{an}的前5项,观察得到最小值b=1+2+3+4+5,a=1+2+4+8+16,计算即可得到a-b的值.
解答 解:由a1=1,an+1-an∈{a1,a2,…,an}(n∈N+),
可得a2-a1=a1,解得a2=2a1=2,
又a3-a2∈{a1,a2},可得a3=a2+a1=3或2a2=4,
又a4-a3∈{a1,a2,a3},可得a4=a3+a1=4或5;
a4=a3+a2=5或6;或a4=2a3=6或8;
又a5-a4∈{a1,a2,a3,a4},可得a5=a4+a1=5或6或7;
a5=a4+a2=6或7或8;a5=a4+a3=7或8或9或10或12;
a5=2a3=8或10或12或16.
综上可得S5的最大值a=1+2+4+8+16=31,
最小值为b=1+2+3+4+5=15.
则a-b=16.
故答案为:16.
点评 本题考查数列的和的最值,注意运用元素与集合的关系,运用列举法,考查判断能力和运算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 气温°C | 14 | 9 | 6 | -5 |
| 茶销售量(杯) | 34 | 44 | 48 | 74 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
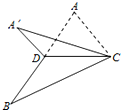 如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A1CD,所成二面角A1-CD-B的平面角为α,则( )
如图,已知△ABC,D是AB的中点,沿直线CD将△ACD折成△A1CD,所成二面角A1-CD-B的平面角为α,则( )| A. | ∠A1CB≥α | B. | ∠A1DB≤α | C. | ∠A1DB≥α | D. | ∠A1CB≤α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
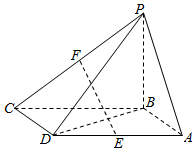 如图,四棱锥P-ABCD的底面ABCD是平行四边形,PB⊥面ABCD,BA=BD=$\sqrt{2}$,AD=2,E,F分别是棱AD,PC的中点.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,PB⊥面ABCD,BA=BD=$\sqrt{2}$,AD=2,E,F分别是棱AD,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -ln2-1 | B. | -1+ln2 | C. | -ln2 | D. | ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com