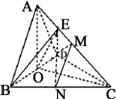
在四面体ABCD中,△BCD是边长为2的正三角形,面ABD面⊥BCD,面ABC⊥面ADC,M、N分别是AC、BC的中点.
(1)过三点D,M,N的平面α与面ABD交于直线l,求证:l∥MN;
(2)若AB=AD,求四面体ABCD的体积.
(1)证明:∵M、N分别是AC、BC的中点,∴MN∥AB
∵MN?面ABD,AB?面ABD
∴MN∥面ABD (2分)
又MN?面α,α∩面ABD=l,
∴l∥MN (4分)
(2)解:如图取BD中点O,连AO、CO,
∵AB=AD,△BCD为正三角形 (6分)
∴AO⊥BD,OC⊥BD,
又面ABD⊥面BCD,∴AO⊥面BCD (8分)
过B作BE⊥AC,连接DE,因为△ADC≌△ABC,所以DE⊥AC,连接OE,由面ABC⊥面ADC,得BE⊥DE (9分)
在等腰Rt△BED中,由BD=2得OE=1,
在Rt△OEC中,OC=

,所以
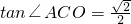
,
在Rt△AOC中,由OC=

,
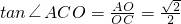
,得OA=

(12分)
∴V
四面体ABCD=
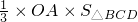
=
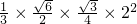
=

(13分)
分析:(1)利用三角形中位线的性质,证明MN∥AB,利用线面平行的判定与性质可得l∥MN;
(2)取BD中点O,连AO、CO,过B作BE⊥AC,连接DE,可得BE⊥DE,从而可求四面体ABCD的体积.
点评:本题考查线面平行的判定与性质,考查四面体的体积,考查学生分析、计算能力,属于中档题.

 (1)证明:∵M、N分别是AC、BC的中点,∴MN∥AB
(1)证明:∵M、N分别是AC、BC的中点,∴MN∥AB ,所以
,所以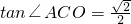 ,
, ,
,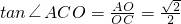 ,得OA=
,得OA= (12分)
(12分)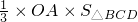 =
=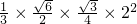 =
= (13分)
(13分)
