
分析 (1)利用已知,将$\overrightarrow a$+$\overrightarrow b$平方展开得到$\overrightarrow a•\overrightarrow b$=0,只要求|$\overrightarrow a$-$\overrightarrow b$|的平方,再开方求值;
(2)结合(1),利用数量积公式,可求向量的夹角.
解答 解:(1)∵$\overrightarrow a$+$\overrightarrow b$=($\sqrt{3}$,1),∴|$\overrightarrow a$+$\overrightarrow b$|=2,∴${\overrightarrow a^2}+2\overrightarrow a•\overrightarrow b+{\overrightarrow b^2}=4$,…(4分)
∵|$\overrightarrow a$|=1,|$\overrightarrow b$|=$\sqrt{3}$,∴$\overrightarrow a•\overrightarrow b$=0,…(2分)
∴|$\overrightarrow a$-$\overrightarrow b$|2=${\overrightarrow a^2}-2\overrightarrow a•\overrightarrow b+{\overrightarrow b^2}=4$
∴|$\overrightarrow a$-$\overrightarrow b$|=2,…(2分)
(2)设$\overrightarrow a$+$\overrightarrow b$ 与$\overrightarrow a$-$\overrightarrow b$ 的夹角为θ ( 0≤θ≤π ),…(1分)
∴cosθ=$\frac{(\overrightarrow a+\overrightarrow b)(\overrightarrow a-\overrightarrow b)}{|\overrightarrow a+\overrightarrow b|•|\overrightarrow a-\overrightarrow b|}=\frac{{{{\overrightarrow a}^2}-{{\overrightarrow b}^2}}}{|\overrightarrow a+\overrightarrow b|•|\overrightarrow a-\overrightarrow b|}=\frac{1-3}{2×2}=-\frac{1}{2}$ …(3分)
∵0≤θ≤π,∴θ=$\frac{2π}{3}$
∴$\overrightarrow a$+$\overrightarrow b$ 与$\overrightarrow a$-$\overrightarrow b$ 的夹角$\frac{2π}{3}$. …(2分)
点评 本题考查了向量的平方与其哦的平方相等、数量积公式的运用求向量夹角.


科目:高中数学 来源: 题型:选择题
| 感染 | 未感染 | 总计 | |
| 服用 | 10 | 40 | 50 |
| 未服用 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.706 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗有关” | |
| B. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗无关” | |
| C. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗有关” | |
| D. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>-1} | B. | {x|-1<x<1} | C. | {x|0<x<1} | D. | {x|-1<x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
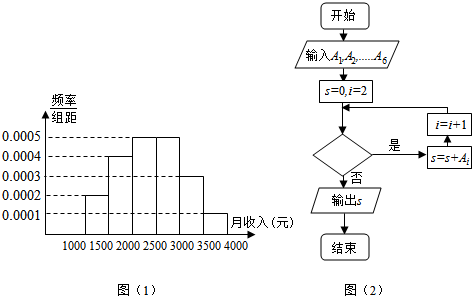
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com