
如图,在直三棱柱 中,
中, ,且
,且 .
.
(Ⅰ)求证:平面 ⊥平面
⊥平面 ;
;
(Ⅱ)设 是
是 的中点,判断并证明在线段
的中点,判断并证明在线段 上是否存在点
上是否存在点 ,使
,使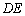 ‖平面
‖平面 ;若存在,求三
;若存在,求三
棱锥 的体积.
的体积.
科目:高中数学 来源: 题型:
下列四个命题中,正确的有
①两个变量间的相关系数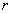 越小,说明两变量间的线性相关程度越低;
越小,说明两变量间的线性相关程度越低;
②命题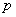 :“
:“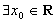 ,
,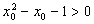 ”的否定
”的否定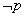 :“
:“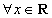 ,
,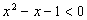 ”;
”;
③用相关指数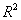 来刻画回归效果,若
来刻画回归效果,若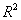 越大,则说明模型的拟合效果越好;
越大,则说明模型的拟合效果越好;
④若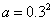 ,
,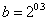 ,
,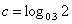 ,则
,则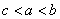 .
.
A.①③④ B.①④ C.③④ D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
已知
 ,且
,且 为偶函数,方程
为偶函数,方程 有两个相等的实数根.
有两个相等的实数根.
(I)求函数 的解析式;
的解析式;
(II)是否存在区间
 ,使得
,使得 在区间
在区间 上的值域为
上的值域为 ?若存在,求
?若存在,求 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
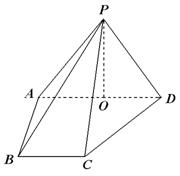
如图,在四棱锥P-ABCD中,侧面PAD 底面ABCD,侧棱PA=PD=
底面ABCD,侧棱PA=PD=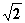 ,底面ABCD为直角梯形,其中BC∥AD,AB
,底面ABCD为直角梯形,其中BC∥AD,AB AD,AD=2AB=2BC=2,O为AD中点。
AD,AD=2AB=2BC=2,O为AD中点。
 ⑴求证:PO
⑴求证:PO 平面ABCD;
平面ABCD;
⑵求异面直线PB与CD所成角的余弦值;
⑶线段AD上是否存在点Q,使得它到平面PCD的距离为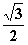 ?若存在,求出
?若存在,求出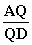 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com