
【题目】设函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,
时,![]() 的零点个数;
的零点个数;
(2)若![]() 的整数解有且唯一,求
的整数解有且唯一,求![]() 的取值范围.
的取值范围.
【答案】(1)只有一个零点(2)![]()
【解析】
(1)求导,根据导数求函数的单调性,结合极值即可判断;(2)易发现![]() ,再分
,再分![]() 和
和![]() 根据导数与函数单调性的关系讨论题设成立时
根据导数与函数单调性的关系讨论题设成立时![]() 的取值范围,求交集即可.
的取值范围,求交集即可.
解:(1)![]() ,当
,当![]() 时,
时,![]() ,函数单增,
,函数单增,
且![]() 时函数值都已经大于0了;当
时函数值都已经大于0了;当![]() 时,
时,![]() ,函数单减,
,函数单减,
且![]() ,所以只有一个零点
,所以只有一个零点
(2)观察发现![]() ,下证除整数0外再无其他整数
,下证除整数0外再无其他整数 ![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 根据同向不等式乘法得到
根据同向不等式乘法得到![]() ,因为
,因为![]() ,
,
所以![]() ,所以函数单增,且
,所以函数单增,且![]() 趋于
趋于![]() 时函数值显然很大很大;
时函数值显然很大很大;
但要保证只有唯一整数0,需要![]() ,却发现恒成立,
,却发现恒成立,
②当![]() 时,要保证只有唯一整数0,首先需要
时,要保证只有唯一整数0,首先需要![]() ,得到
,得到![]()
当![]() 时,
时,![]() ,
,![]() 根据同向不等式得到
根据同向不等式得到![]() ,又因
,又因![]() ,
,
所以![]() ,所以函数在
,所以函数在![]() 单减,且
单减,且![]()
综上所述:![]() 的整数解有且唯一时,
的整数解有且唯一时,![]()


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,点
,点![]() 是矩形
是矩形![]() 内(含边界)的动点,且
内(含边界)的动点,且![]() ,
,![]() ,直线
,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .记点
.记点![]() 的轨迹长度为
的轨迹长度为![]() ,则
,则![]() ______;当三棱锥
______;当三棱锥![]() 的体积最小时,三棱锥
的体积最小时,三棱锥![]() 的外接球的表面积为______.
的外接球的表面积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前有声书正受着越来越多人的喜爱.某有声书公司为了解用户使用情况,随机选取了![]() 名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
名用户,统计出年龄分布和用户付费金额(金额为整数)情况如下图.
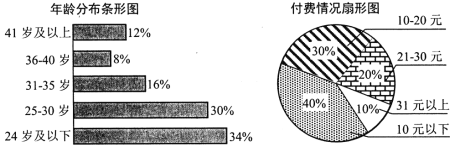
有声书公司将付费高于![]() 元的用户定义为“爱付费用户”,将年龄在
元的用户定义为“爱付费用户”,将年龄在![]() 岁及以下的用户定义为“年轻用户”.已知抽取的样本中有
岁及以下的用户定义为“年轻用户”.已知抽取的样本中有![]() 的“年轻用户”是“爱付费用户”.
的“年轻用户”是“爱付费用户”.
(1)完成下面的![]() 列联表,并据此资料,能否有
列联表,并据此资料,能否有![]() 的把握认为用户“爱付费”与其为“年轻用户”有关?
的把握认为用户“爱付费”与其为“年轻用户”有关?
爱付费用户 | 不爱付费用户 | 合计 | |
年轻用户 | |||
非年轻用户 | |||
合计 |
(2)若公司采用分层抽样方法从“爱付费用户”中随机选取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人进行访谈,求抽取的
人进行访谈,求抽取的![]() 人恰好都是“年轻用户”的概率.
人恰好都是“年轻用户”的概率.
|
|
|
|
|
|
|
|
|
|
|
|
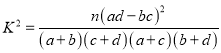 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样检查,测得身高情况的统计图如下:
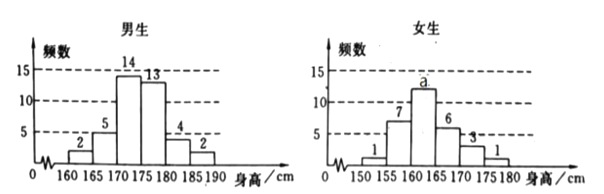
(1)估计该校男生的人数;并求出![]() 值
值
(2)估计该校学生身高在![]() 之间的概率;
之间的概率;
(3)从样本中身高在![]() 之间的女生中任选2人,求至少有1人身高在
之间的女生中任选2人,求至少有1人身高在![]() 之间的概率。
之间的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—5: 不等式选讲
已知函数f(x)=![]() 的定义域为R.
的定义域为R.
(Ⅰ)求实数m的取值范围;
(Ⅱ)若m的最大值为n,当正数a,b满足![]() =n时,求7a+4b的最小值.
=n时,求7a+4b的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com