
【题目】在几何体![]() 中,如图,四边形
中,如图,四边形![]() 为平行四边形,
为平行四边形,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() .
.
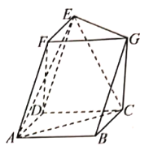
(1)求证:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)由![]() ,得到平面
,得到平面![]() ,平面
,平面![]() ,根据平面
,根据平面![]() 平面
平面![]() ,由面面平行的性质定理得到
,由面面平行的性质定理得到![]() ,进而得到四边形
,进而得到四边形![]() 为平行四边形,再根据
为平行四边形,再根据![]() 平面
平面![]() ,得到
,得到![]() ,由
,由![]() ,得到
,得到![]() ,同理得到
,同理得到![]() ,由线面垂直的判定定理得到
,由线面垂直的判定定理得到![]() 平面
平面![]() 得证.
得证.
(2)由(1)可知,直线![]() 、
、![]() 、
、![]() 两两垂直.以
两两垂直.以![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 、
、![]() 为坐标轴建立的空间直角坐标系
为坐标轴建立的空间直角坐标系![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,分别求得平面
,分别求得平面![]() 和平面
和平面![]() 的一个法向量
的一个法向量![]() ,代入
,代入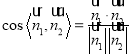 求解.
求解.
(1)证明:由![]() ,
,
可知![]() 、
、![]() 、
、![]() 、
、![]() 四点确定平面
四点确定平面![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 四点确定平面
四点确定平面![]() .
.
∵平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
∴![]() ,四边形
,四边形![]() 为平行四边形.
为平行四边形.
同理可得,四边形![]() 为平行四边形,四边形
为平行四边形,四边形![]() 为平行四边形.
为平行四边形.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
而![]() ,于是
,于是![]() .
.
由![]() ,
,![]() ,
,
则![]() .
.
由![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴![]() .
.
(2)由(1)可知,直线![]() 、
、![]() 、
、![]() 两两垂直.以
两两垂直.以![]() 为坐标原点,以
为坐标原点,以![]() 、
、![]() 、
、![]() 为坐标轴建立的空间直角坐标系
为坐标轴建立的空间直角坐标系![]() .
.
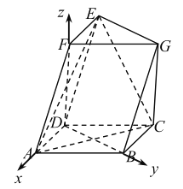
不妨设![]() ,则
,则![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则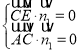 ,则
,则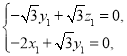 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
∴平面![]() 的一个法向量为
的一个法向量为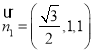 .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则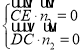 ,则
,则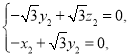 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
∴平面![]() 的一个法向量为
的一个法向量为![]() .
.
∴二面角![]() 的余弦值为
的余弦值为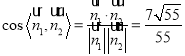 .
.


科目:高中数学 来源: 题型:
【题目】人们通常以分贝(符号是![]() )为单位来表示声音强度的等级,30~40分贝是较理想的安静环境,超过50分贝就会影响睡眠和休息,70分贝以上会干扰谈话,长期生活在90分贝以上的嗓声环境,会严重影响听力和引起神经衰弱、头疼、血压升高等疾病,如果突然暴露在高达150分贝的噪声环境中,听觉器官会发生急剧外伤,引起鼓膜破裂出血,双耳完全失去听力,为了保护听力,应控制噪声不超过90分贝,一般地,如果强度为
)为单位来表示声音强度的等级,30~40分贝是较理想的安静环境,超过50分贝就会影响睡眠和休息,70分贝以上会干扰谈话,长期生活在90分贝以上的嗓声环境,会严重影响听力和引起神经衰弱、头疼、血压升高等疾病,如果突然暴露在高达150分贝的噪声环境中,听觉器官会发生急剧外伤,引起鼓膜破裂出血,双耳完全失去听力,为了保护听力,应控制噪声不超过90分贝,一般地,如果强度为![]() 的声音对应的等级为
的声音对应的等级为![]() ,则有
,则有![]() ,则
,则![]() 的声音与
的声音与![]() 的声音强度之比为( )
的声音强度之比为( )
A.10B.100C.1000D.10000
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与圆
与圆![]() 相外切,且与直线
相外切,且与直线![]() 相切.
相切.
(1)记圆心![]() 的轨迹为曲线
的轨迹为曲线![]() ,求
,求![]() 的方程;
的方程;
(2)过点![]() 的两条直线
的两条直线![]() 与曲线
与曲线![]() 分别相交于点
分别相交于点![]() 和
和![]() ,线段
,线段![]() 和
和![]() 的中点分别为
的中点分别为![]() .如果直线
.如果直线![]() 与
与![]() 的斜率之积等于1,求证:直线
的斜率之积等于1,求证:直线![]() 经过定点.
经过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,若△
,若△![]() 的三个顶点都在抛物线
的三个顶点都在抛物线![]() 上,且
上,且![]() ,则称该三角形为“核心三角形”.
,则称该三角形为“核心三角形”.
(1)是否存在“核心三角形”,其中两个顶点的坐标分别为![]() 和
和![]() ?请说明理由;
?请说明理由;
(2)设“核心三角形”![]() 的一边
的一边![]() 所在直线的斜率为4,求直线
所在直线的斜率为4,求直线![]() 的方程;
的方程;
(3)已知△![]() 是“核心三角形”,证明:点
是“核心三角形”,证明:点![]() 的横坐标小于2.
的横坐标小于2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为![]() 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)直线AP与椭圆在点B处的切线交于点D,当点P在椭圆上运动时,求证:以BD为直径的圆与直线PF恒相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司为客户定制了5个险种:甲,一年期短险;乙,两全保险;丙,理财类保险;丁,定期寿险:戊,重大疾病保险,各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查,得出如下的统计图例,以下四个选项错误的是( )



A.54周岁以上参保人数最少B.18~29周岁人群参保总费用最少
C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com