[题目]已知圆与圆相外切.且与直线相切．(1)记圆心的轨迹为曲线.求的方程,(2)过点的两条直线与曲线分别相交于点和.线段和的中点分别为.如果直线与的斜率之积等于1.求证:直线经过定点．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知圆与圆相外切，且与直线相切．

（1）记圆心的轨迹为曲线，求的方程；

（2）过点的两条直线与曲线分别相交于点和，线段和的中点分别为.如果直线与的斜率之积等于1，求证：直线经过定点．

【答案】（1）（2）见解析

【解析】

（1）根据抛物线定义可知圆心的轨迹为抛物线，进而可得其轨迹方程.

（2）由题意可设直线的斜率为，则直线的斜率为，表示出直线的方程，联立直线与抛物线方程即可求得交点的坐标，进而以代替点坐标中的，可得点的坐标；即可表示出直线的斜率及其方程，进而得所过定点的坐标.

（1）依题意等于到直线的距离，

故所求轨迹是以为焦点，以为准线的抛物线.

故其轨迹的方程为.

（2）依题意直线斜率都存在且均不为，

故设直线的斜率为，则直线的斜率为.

直线的方程为，

即为.

由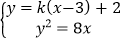消去整理得，

所以，点的坐标为，

以代替点坐标中的，可得点的坐标为，

所以直线的斜率，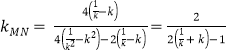

所以直线的方程为，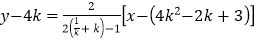

即.

故经过定点.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】“业务技能测试”是量化考核员工绩效等级的一项重要参考依据．某公司为量化考核员工绩效等级设计了A，B两套测试方案，现各抽取名员工参加A，B两套测试方案的预测试，统计成绩（满分分），得到如下频率分布表．

成绩频率
方案A
方案B

（1）从预测试成绩在的员工中随机抽取人，记参加方案A的人数为，求的最有可能的取值；

（2）由于方案A的预测试成绩更接近正态分布，该公司选择方案A进行业务技能测试．测试后，公司统计了若干部门测试的平均成绩与绩效等级优秀率，如下表所示：

根据数据绘制散点图，初步判断，选用作为回归方程．令，经计算得，，．

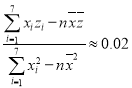（ⅰ）若某部门测试的平均成绩为，则其绩效等级优秀率的预报值为多少？

（ⅱ）根据统计分析，大致认为各部门测试平均成绩，其中近似为样本平均数，近似为样本方差，求某个部门绩效等级优秀率不低于的概率为多少？

参考公式与数据：（1），，．

（2）线性回归方程中，，．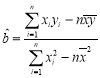

（3）若随机变量，则，，．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知数列{an}是单调递增的等差数列，a2+a4＝14且a2﹣1，a3+1，a4+7成等比数列．

（1）求数列{an}的通项公式；

（2）设数列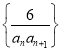的前n项和为Sn．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】四棱锥的底面是边长的菱形，，的中点是顶点在底面的射影，是的中点.

(1)求证：面平面；

(2)若，求面角的余弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在几何体中，如图，四边形为平行四边形，，平面平面，平面，，.

（1）求证：；

（2）求二面角的余弦值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】当急需住院人数超过医院所能收治的病人数量时就会发生“医疗资源挤兑”现象，在新冠肺炎爆发期间，境外某市每日下班后统计住院人数，从中发现：该市每日因新冠肺炎住院人数均比前一天下班后统计的住院人数增加约25%，但每日大约有200名新冠肺炎患者治愈出院，已知该市某天下班后有1000名新冠肺炎患者住院治疗，该市的医院共可收治4000名新冠肺炎患者，若继续按照这样的规律发展，该市因新冠肺炎疫情发生“医疗资源挤兑”现象，只需要约（）

参考数据：.