
【题目】已知椭圆![]() (常数a,b>0,且a>b)的左、右焦点分别为F1,F2,M,N为短轴的两个端点,且四边形F1MF2N是面积为4的正方形.
(常数a,b>0,且a>b)的左、右焦点分别为F1,F2,M,N为短轴的两个端点,且四边形F1MF2N是面积为4的正方形.
(1)求椭圆的方程;
(2)过原点且斜率分别为k和-k(k≥2)的两条直线与椭圆![]() 的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值.
的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由四边形F1MF2N是面积为4的正方形,可得关于a,b的方程组,即可得到椭圆的方程;(2)设A(x,y),求出A点坐标.根据题意设直线图象与椭圆的对称性,知![]() ,结合均值不等式即可得到四边形ABCD的面积S的最大值.
,结合均值不等式即可得到四边形ABCD的面积S的最大值.
试题解析:
(1)依题意得![]() ∴
∴![]() 所求椭圆方程为
所求椭圆方程为![]() +
+![]() =1.
=1.
(2)设A(x,y),由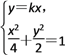 得A(
得A(![]() ,
,![]() ),
),
根据题设直线图象与椭圆的对称性,知S=4×![]() ×
×![]() =
=![]() (k≥2),
(k≥2),
∴S=![]() (k≥2),
(k≥2),
设M(k)=2k+![]() ,则M ′(k)=2-
,则M ′(k)=2-![]() ,当k≥2时,M ′(k)=2-
,当k≥2时,M ′(k)=2-![]() >0,
>0,
∴M(k)在k∈[2,+∞)时单调递增,∴M(k)min=M(2)=![]() , 所以当k≥2时,Smax=
, 所以当k≥2时,Smax=![]() =
=![]() .
.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线![]() =1(a>0,b>0)的右焦点为F(c,0).
=1(a>0,b>0)的右焦点为F(c,0).
(1)若双曲线的一条渐近线方程为y=x且c=2,求双曲线的方程;
(2)以原点O为圆心,c为半径作圆,该圆与双曲线在第一象限的交点为A,过A作圆的切线,斜率为-![]() ,求双曲线的离心率.
,求双曲线的离心率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,设
,设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校推广新课改,在两个程度接近的班进行试验,一班为新课改班级,二班为非课改班级,经过一个学期的教学后对期末考试进行分析评价,规定:总分超过550(或等于550分)为优秀,550以下为非优秀,得到以下列联表:
优秀 | 非优秀 | 合计 | |
一班 | 35 | 13 | |
二班 | 25 | ||
合计 | 90 |
(1)请完成上面的列联表;
(2)根据列联表的数据,能否在犯错误的概率不超过0.005的前提下认为推广新课改与数学成绩有关系?
参考数据:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
k2=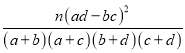
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点, ![]() 轴非负半轴为极轴建立极坐标系.
轴非负半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的极坐标方程为
的极坐标方程为![]() ,射线
,射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=![]() ,其前n项和为Sn,且Sn=an+1-
,其前n项和为Sn,且Sn=an+1-![]() (n∈N*).
(n∈N*).
(1)求an,Sn;
(2)设bn=log2(2Sn+1)-2,数列{cn}满足cn·bn+3·bn+4=1+(n+1)(n+2)·2bn,数列{cn}的前n项和为Tn,求使4Tn>2n+1-![]() 成立的最小正整数n的值.
成立的最小正整数n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣1|+|2x+3|.
(1)解不等式f(x)≥6;
(2)记f(x)的最小值是m,正实数a,b满足2ab+a+2b=m,求a+2b的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com