
【题目】某农科所发现,一种作物的年收获量![]() (单位:
(单位:![]() )与它“相近”作物的株数
)与它“相近”作物的株数![]() 具有相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有相关关系(所谓两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近作物的株数为
),并分别记录了相近作物的株数为![]() 时,该作物的年收获量的相关数据如下:
时,该作物的年收获量的相关数据如下:
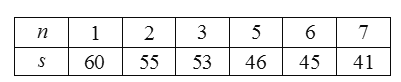
(1)根据研究发现,该作物的年收获量![]() 可能和它“相近”作物的株数
可能和它“相近”作物的株数![]() 有以下两种回归方程:
有以下两种回归方程:![]() ,利用统计知识,结合相关系数
,利用统计知识,结合相关系数![]() 比较使用哪种回归方程更合适;
比较使用哪种回归方程更合适;
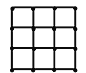
(2)农科所在如下图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株该作物,其中每个小正方形的面积为![]() ,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收获量以(1)中选择的回归方程计算所得数据为依据)
,若在所种作物中随机选取一株,求它的年收获量的分布列与数学期望.(注:年收获量以(1)中选择的回归方程计算所得数据为依据)
参考公式:线性回归方程为![]() ,其中
,其中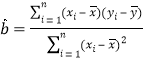 ,
,![]() ,
,
相关系数 ;
;
参考数值:![]() ,
,![]() ,
,![]() ,其中
,其中![]() .
.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】以下命题正确的是( )
A. 若直线![]() ,
,![]() ,
,![]() ,则直线a,b异面
,则直线a,b异面
B. 空间内任意三点可以确定一个平面
C. 空间四点共面,则其中必有三点共线
D. 直线![]() ,
,![]() ,
,![]() ,则直线a,b异面
,则直线a,b异面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】红外线治疗仪的治疗作用是在红外线照射下,组织温度升高,毛细血管扩张,血流加快,物质代谢增强,组织细胞活力及再生能力提高,对我们身体某些疾病的治疗有着很大的贡献,某药店兼营某种红外线治疗仪,经过近![]() 个月的营销,对销售状况进行相关数据分析,发现月销售量与销售价格有关,其统计数据如下表:
个月的营销,对销售状况进行相关数据分析,发现月销售量与销售价格有关,其统计数据如下表:
每台红外线治疗仪的销售价格: |
|
|
|
|
|
红外线治疗仪的月销售量: |
|
|
|
|
|
(1)根据表中数据求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)①每台红外线治疗仪的价格为![]() 元时,预测红外线治疗仪的月销售量;(四舍五入为整数)
元时,预测红外线治疗仪的月销售量;(四舍五入为整数)
②若该红外线治疗仪的成本为![]() 元/台,药店为使每月获得最大的纯收益,利用(1)中结论,问每台该种红外线治疗仪的销售价格应定为多少元?(四舍五入,精确到
元/台,药店为使每月获得最大的纯收益,利用(1)中结论,问每台该种红外线治疗仪的销售价格应定为多少元?(四舍五入,精确到![]() 元).
元).
参考公式:回归直线方程![]() ,
,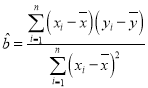 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数(consumer price index)的简称.居民消费价格指数,是一个反映居民家庭一般所购买的消费品价格水平变动情况的宏观经济指标.右图是根据统计局发布的2018年1月—7月的CPI 同比增长与环比增长涨跌幅数据绘制的折线图.(注:2018 年2月与2017年2月相比较,叫同比;2018年2 月与2018年1月相比较,叫环比)根据该折线图,则下列结论错误的是( )
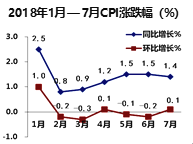
A. 2018年1月—7月CPI 有涨有跌
B. 2018年2月—7月CPI 涨跌波动不大,变化比较平稳
C. 2018年1月—7月分别与2017年1月一7月相比较,1月CPI 涨幅最大
D. 2018年1月—7月分别与2017年1月一7月相比较,CPI 有涨有跌
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,国家深入推进精准脱贫,加大资金投入,强化社会帮扶,为了更好的服务于人民,派调查组到某农村去考察和指导工作.该地区有200户农民,且都从事水果种植,据了解,平均每户的年收入为3万元.为了调整产业结构,调查组和当地政府决定动员部分农民从事水果加工,据估计,若能动员![]() 户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高
户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高![]() ,而从事水果加工的农民平均每户收入将为
,而从事水果加工的农民平均每户收入将为![]() 万元.
万元.
(1)若动员![]() 户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求
户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这200户农民中从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中
(其中![]() ,
,![]() ,
,![]() )的图象与
)的图象与![]() 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为![]() ,且图象上一个最高点为
,且图象上一个最高点为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)先把函数![]() 的图象向左平移
的图象向左平移![]() 个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数
个单位长度,然后再把所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变),得到函数![]() 的图象,试写出函数
的图象,试写出函数![]() 的解析式.
的解析式.
(3)在(2)的条件下,若存在![]() ,使得不等式
,使得不等式![]() 成立,求实数
成立,求实数![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上奇函数f(x)在![]() 时的图象是如图所示的抛物线的一部分.
时的图象是如图所示的抛物线的一部分.

(1)请补全函数f(x)的图象;
(2)写出函数f(x)的表达式;
(3)讨论方程|f(x)|=a的解的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】口袋里装有1红,2白,3黄共6个形状相同的小球,从中取出2球,事件![]() “取出的两球同色”,
“取出的两球同色”,![]() “取出的2球中至少有一个黄球”,
“取出的2球中至少有一个黄球”,![]() “取出的2球至少有一个白球”,
“取出的2球至少有一个白球”,![]() “取出的两球不同色”,
“取出的两球不同色”,![]() “取出的2球中至多有一个白球”.下列判断中正确的序号为________.
“取出的2球中至多有一个白球”.下列判断中正确的序号为________.
①![]() 与
与![]() 为对立事件;②
为对立事件;②![]() 与
与![]() 是互斥事件;③
是互斥事件;③![]() 与
与![]() 是对立事件:④
是对立事件:④![]() ;⑤
;⑤![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com