
分析 利用向量垂直,数量积为0,得到两个向量的模相等;向量的模等于坐标平方和的算术平方根.
解答 解:因为($\overrightarrow{a}$+$\overrightarrow{b}$)⊥($\overrightarrow{a}$-$\overrightarrow{b}$),所以($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=0,所以${\overrightarrow{a}}^{2}-{\overrightarrow{b}}^{2}$=0,所以|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=$\sqrt{{1}^{2}+(-1)^{2}}=\sqrt{2}$;
故答案为:$\sqrt{2}$.
点评 本题考查了向量垂直的性质以及向量模的求法,属于基础题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{9}{25}$ | D. | $\frac{16}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{7}$ | B. | $24\sqrt{7}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{21}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2017届四川成都七中高三10月段测数学(文)试卷(解析版) 题型:填空题
已知三次函数 ,下列命题正确的是 .
,下列命题正确的是 .
①函数 关于原点
关于原点 中心对称;
中心对称;
②以 ,
, 两不同的点为切点作两条互相平行的切线,分别与
两不同的点为切点作两条互相平行的切线,分别与 交于
交于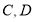 两点,则这四个点的横坐标满足关系
两点,则这四个点的横坐标满足关系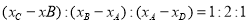 ;
;
③以 为切点,作切线与
为切点,作切线与 图像交于点
图像交于点 ,再以点
,再以点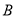 为切点作直线与
为切点作直线与 图像交于点
图像交于点 ,再以点
,再以点 作切点作直线与
作切点作直线与 图像交于点
图像交于点 ,则
,则 点横坐标为
点横坐标为 ;
;
④若 ,函数
,函数 图像上存在四点
图像上存在四点 ,使得以它们为顶点的四边形有且仅有一个正方形.
,使得以它们为顶点的四边形有且仅有一个正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com