
(1)y=x2+![]() ;(2)y=|x+1|+|x-1|.
;(2)y=|x+1|+|x-1|.
思路分析:本题主要考查函数的最值及其求法.对于不同的函数采用不同的求法.(1)利用函数的单调性求最值;(2)可以画图像,也可以对解析式赋予几何意义,数形结合求最值.
解:(1)(单调法)函数y=x2+![]() 的定义域是[0,+∞),可以证明函数y=x2+
的定义域是[0,+∞),可以证明函数y=x2+![]() 在定义域内是增函数,则有f(x)≥f(0)=0+0=0,即函数y=x2+x有最小值0,无最大值.
在定义域内是增函数,则有f(x)≥f(0)=0+0=0,即函数y=x2+x有最小值0,无最大值.
(2)解法一(图像法):y=|x+1|+|x-1|=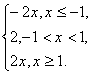 其图像如图所示.
其图像如图所示.
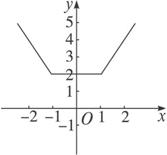
由图像得函数的最小值是2,无最大值;
解法二(数形结合):函数的解析式y=|x+1|+|x-1|的几何意义是:y是数轴上任意一点P到±1的对应点A,B的距离的和,即y=|PA|+|PB|,如图所示,
![]()
观察数轴可得|PA|+|PB|≥|AB|=2,即函数有最小值2,无最大值.


科目:高中数学 来源: 题型:
| 4 |
| x |
| 1 |
| x-2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 6 |
| x2 |
| 1 |
| 9 |
| x |
| 27 |
| 1 |
| b(a-b) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com