
| A. | $\frac{2}{5}$ | B. | $\frac{16}{25}$ | C. | $\frac{17}{25}$ | D. | $\frac{23}{25}$ |
分析 本题是一个等可能事件的概率,试验发生包含的事件是在区间[0,1]上任取两个数a和b,写出事件对应的集合,做出面积,满足条件的事件是a+b<$\frac{8}{5}$,写出对应的集合,做出面积,得到概率.
解答 解:由题意知本题是一个等可能事件的概率,
∵试验发生包含的事件是在区间[0,1]上任取两个数a和b,
事件对应的集合是Ω={(a,b)|0≤a≤1,0≤b≤1}
对应的面积是sΩ=1
满足条件的事件是a+b<$\frac{8}{5}$,事件对应的集合是A={(a,b)|0≤a≤1,0≤b≤1,a+b<$\frac{8}{5}$}
对应的图形的面积是sA=1-$\frac{1}{2}×\frac{2}{5}×\frac{2}{5}$=1-$\frac{2}{25}$=$\frac{23}{25}$
∴根据等可能事件的概率得到P=$\frac{23}{25}$,
故选D.
点评 本题考查等可能事件的概率,是一个几何概型,几何概型的概率的值是通过长度、面积、和体积、的比值得到结果,是一个基础题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
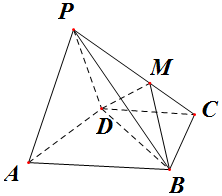 如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.
如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2或$\frac{2}{55}$ | B. | -2 | C. | 2 | D. | 2或$-\frac{2}{55}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {0,1,2,3} | C. | {1,2} | D. | {0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com