
【题目】已知等比数列{an}的各项均为正数,2a2﹣5a1=3,a3a7=9a42;
(1)求数列{an}的通项公式;
(2)设bn=anlog3an,求数列{bn}的前n项和Sn.
科目:高中数学 来源: 题型:
【题目】如图,在长方![]() 中,
中,![]() ,
,![]() ,E为
,E为![]() 的中点,以
的中点,以![]() 为折痕,把
为折痕,把![]() 折起到
折起到![]() 的位置,且平面
的位置,且平面![]() 平面
平面![]() .
.

(1)求证:![]() ;
;
(2)在棱![]() 上是否存在一点P,使得
上是否存在一点P,使得![]() 平面
平面![]() ,若存在,求出点P的位置,若不存在,请说明理由.
,若存在,求出点P的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
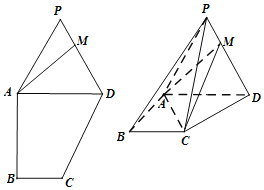
【题目】如图,在多边形PABCD中,![]() ,
,![]() ,
,![]() ,
,![]() ,M是线段PD上的一点,且
,M是线段PD上的一点,且![]() ,若将
,若将![]() 沿AD折起,得到几何体
沿AD折起,得到几何体![]() .
.
![]() 证明:
证明:![]() 平面AMC
平面AMC
![]() 若
若![]() ,且平面
,且平面![]() 平面ABCD,求三棱锥
平面ABCD,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一只药用昆虫的产卵数y与一定范围内的温度x有关,现收集了该种药用昆虫的6组观测数据如下表:
温度x/℃ | 21 | 23 | 24 | 27 | 29 | 32 |
产卵数y/个 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算得:
![]() ,
,![]() ,
,![]() 线性回归模型的残差平方和
线性回归模型的残差平方和![]() ,
,![]() ,
,
其中![]() 分别为观测数据中的温度和产卵数,
分别为观测数据中的温度和产卵数,![]()
(1)若用线性回归模型,求y关于x的回归方程![]() (精确到0.1);
(精确到0.1);
(2)若用非线性回归模型求得y关于x的回归方程为![]() ,且相关指数
,且相关指数![]() .
.
①试与1中的回归模型相比,用![]() 说明哪种模型的拟合效果更好.
说明哪种模型的拟合效果更好.
②用拟合效果好的模型预测温度为35℃时该用哪种药用昆虫的产卵数(结果取整数)
附:一组数据![]() 其回归直线
其回归直线![]() 的斜率和截距的最小二乘估计为
的斜率和截距的最小二乘估计为 ,
,![]() ;相关指数
;相关指数 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com