练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．已知“0＜t＜m（m＞0）”是“函数f（x）=-x2-tx+3t在区间（0，2）上只有一个零点”的充分不必要条件，求实数m的取值范围．

    分析 先根据函数f（x）解析式求出该函数在（0，2）上存在零点时t的取值范围：0＜t＜4，所以由0＜t＜m（m＞0）是f（x）在（0，2）上存在一个零点的充分不必要条件，得到：0＜m＜4．

    解答 解：对于函数f（x）=-x2-tx+3t，在区间（0，2）上只有一个零点时，
    只能△=t2+12t＞0，即t＜-12，或t＞0；
    此时，f（0）f（2）=3t（t-4）＜0，解得0＜t＜4；
    ∵0＜t＜m（m＞0）是函数f（x）在（0，2）上只有一个零点的充分不必要条件；
    ∴0＜m＜4．

    点评 本题考查函数零点的概念，二次函数图象和x轴交点的情况和判别式△的关系，充分条件，必要条件，充分不必要条件的概念．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．若不等式组$\left\{{\begin{array}{l}{x-y+2≥0}\\{x-5y+10≤0}\\{x+y-8≤0}\end{array}}\right.$，表示的平面区域为D，则将D绕原点旋转一周所得区域的面积为（　　）
    A．30πB．28πC．26πD．25π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．命题p：关于x的不等式x2+（a-1）x+a2＜0的解集是空集，命题q：已知二次函数f（x）=x2-mx+2满足$f（\frac{3}{2}+x）=f（\frac{3}{2}-x）$，且当x∈[0，a]时，最大值是2，若命题“p且q”为假，“p或q”为真，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

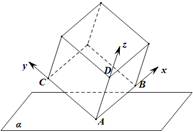    6．如图，棱长为3的正方体的顶点A在平α上，三条棱AB、AC、AD都在平面α的同侧．若顶点B，C到平面α的距离分别为1，$\sqrt{2}$．建立如图所示的空间直角坐标系，设平面α的一个法向量为（x0，y0，z0），若x0=1，则y0=$\sqrt{2}$，z0=$\sqrt{6}$，且顶点D到平面α的距离是$\sqrt{6}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．已知函数g（x）=log2（x-1），f（x）=log${\;}_{\frac{1}{2}}$（x+1），
    （1）求不等式g（x）≥f（x）的解集；
    （2）在（1）的条件下求函数y=g（x）+f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．画出函数y=$\frac{x+3}{x+2}$的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

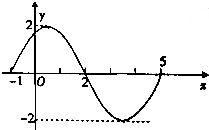    10．如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的一部分图象．
    （1）写出f（x）的解析式；
    （2）若将f（x）的图象向右平移1个单位得到的g（x）的图象，求函数g（x）的单调递增区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．如图，边长为2的正方形ABCD中，BE=BF=$\frac{1}{4}$BC，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于A′点，则三棱锥A′-EFD的体积为（　　）
    A．$\frac{{\sqrt{21}}}{12}$B．$\frac{{\sqrt{17}}}{12}$C．$\frac{{\sqrt{21}}}{6}$D．$\frac{{\sqrt{17}}}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知x，y满足约束条件$\left\{\begin{array}{l}{x-y＞2}\\{x+y≤2}\\{y≥-2}\end{array}\right.$，则z=3x+y的取值范围为（　　）
    A．[-2，10）B．（-2，10]C．[6，10]D．（6，10]

    查看答案和解析>>

    同步练习册答案