
分析 对于命题p:由关于x的不等式x2+(a-1)x+a2<0的解集是空集,可得△≤0,解得p的取值范围.由已知得二次函数f(x)=x2-mx+2的对称轴为$x=\frac{3}{2}$,可得m,可得f(x)=x2-3x+2,当x∈[0,a]时,最大值是2,由对称性知a的取值范围.由命题“p且q”为假,“p或q”为真,可知:p,q恰一真一假.
解答 解:对于命题p:∵关于x的不等式x2+(a-1)x+a2<0的解集是空集,
∴△=-3a2-2a+1≤0,解得$p:a≤-1\;或a≥\frac{1}{3}$,
由已知得二次函数f(x)=x2-mx+2的对称轴为$x=\frac{3}{2}$,
即$-\frac{-m}{2}=\frac{3}{2}$,∴m=3,f(x)=x2-3x+2,
当x∈[0,a]时,最大值是2,由对称性知q:0<a≤3.
由命题“p且q”为假,“p或q”为真,可知:p,q恰一真一假.
当p真q假时,$\left\{{\begin{array}{l}{a≤-1\;或a≥\frac{1}{3}}\\{a≤0\;或a>3}\end{array}}\right.$,∴a≤-1或a>3,
当p假q真时,$\left\{{\begin{array}{l}{-1<a<\frac{1}{3}}\\{0<a≤3}\end{array}}\right.$,∴$0<a<\frac{1}{3}$,
综上可得,$a∈(-∞,-1]∪(0,\frac{1}{3})∪(3,+∞)$.
点评 本题考查了简易逻辑的判定方法、一元二次不等式的解法、二次函数的单调性和对称性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -4 | C. | -9 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
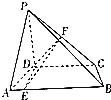 如图,四边形ABCD为等腰梯形,PD⊥平面ABCD,F为PC的中点,CD=AD=PD,AB=4AE=2CD.
如图,四边形ABCD为等腰梯形,PD⊥平面ABCD,F为PC的中点,CD=AD=PD,AB=4AE=2CD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 相关人员数 | 抽取人数 | |
| 公务员 | 32 | x |
| 教师 | 48 | y |
| 自由职业者 | 64 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com