
���� ��1������C�IJ�������Ϊ��$\left\{\begin{array}{l}{x=\sqrt{3}cos��}\\{y=sin��}\end{array}\right.$ ����Ϊ������������ƽ����ϵ�ɵ���ͨ���̣�ֱ��l�ļ����귽��Ϊ��2��cos����+$\frac{��}{3}$��+3$\sqrt{6}$=0��չ���ɵã�2��$��\frac{1}{2}cos��-\frac{\sqrt{3}}{2}sin�ȣ�$+3$\sqrt{6}$=0�����û�����ʽ�ɵ�ֱ�����귽�̣�
��2����P$��\sqrt{3}cos�ȣ�sin�ȣ�$�����õ㵽ֱ�ߵľ��빫ʽ�ɵã���P��ֱ��l�ľ���d=$\frac{\sqrt{6}|sin����-\frac{��}{4}��-3|}{2}$�����������Ǻ����ĵ�������ֵ�ɵó���
��� �⣺��1������C�IJ�������Ϊ��$\left\{\begin{array}{l}{x=\sqrt{3}cos��}\\{y=sin��}\end{array}\right.$ ����Ϊ��������
�ɵ���ͨ���̣�$\frac{{x}^{2}}{3}$+y2=1��
ֱ��l�ļ����귽��Ϊ��2��cos����+$\frac{��}{3}$��+3$\sqrt{6}$=0��
չ���ɵã�2��$��\frac{1}{2}cos��-\frac{\sqrt{3}}{2}sin�ȣ�$+3$\sqrt{6}$=0��
����x-$\sqrt{3}$y+3$\sqrt{6}$=0��
��2����P$��\sqrt{3}cos�ȣ�sin�ȣ�$��
��P��ֱ��l�ľ���d=$\frac{|\sqrt{3}cos��-\sqrt{3}sin��+3\sqrt{6}|}{2}$=$\frac{\sqrt{6}|sin����-\frac{��}{4}��-3|}{2}$��$\frac{\sqrt{6}��2}{2}$=$\sqrt{6}$��
��sin$����-\frac{��}{4}��$=1ʱȡ�Ⱥţ�
���P��ֱ��l�ľ������Сֵ��$\sqrt{6}$��
���� ���⿼���˲������̻�Ϊ��ͨ���̡������귽�̻�Ϊֱ�����귽�̡�ƽ����ϵ�����Ǻ����ĵ�������ֵ������������������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
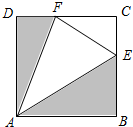 һλ��ҵ����������һ��߳�Ϊ1�������������ABCD�����䡢���������ۣ����������εı�BC��CD�Ϸֱ�ȡ��E��F�����������εĶ����غϣ�������AE��EF��FA��ʹ�á�EAF=45�㣮���⽫ͼ����Ӱ���ֹ滮Ϊ��Դֲ������������AEF���ֹ滮Ϊ�䳲������CEF���ֹ滮Ϊ���۽�����������Դֲ����������Ͷ��ԼΪ2��105Ԫ/����2���䳲������۽�������Ͷ��ԼΪ105Ԫ/����2�����������������Ͷ��������Ҫ����Ԫ��
һλ��ҵ����������һ��߳�Ϊ1�������������ABCD�����䡢���������ۣ����������εı�BC��CD�Ϸֱ�ȡ��E��F�����������εĶ����غϣ�������AE��EF��FA��ʹ�á�EAF=45�㣮���⽫ͼ����Ӱ���ֹ滮Ϊ��Դֲ������������AEF���ֹ滮Ϊ�䳲������CEF���ֹ滮Ϊ���۽�����������Դֲ����������Ͷ��ԼΪ2��105Ԫ/����2���䳲������۽�������Ͷ��ԼΪ105Ԫ/����2�����������������Ͷ��������Ҫ����Ԫ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | ������ | �ܼ� | |
| �װ� | 10 | ||
| �Ұ� | 30 | ||
| �ϼ� | 100 |
| p��K2��k0�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-1��1] | B�� | ��-3��3�� | C�� | ��-3��-1]��[1��3�� | D�� | ��-3��-1���ȣ�1��3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | n•2n | B�� | ��n-1��•2n-1-1 | C�� | ��n-1��•2n+1 | D�� | 2n+1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com