
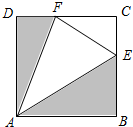
 一位创业青年租用了一块边长为1百米的正方形田地ABCD来养蜂、产蜜与售蜜,他在正方形的边BC,CD上分别取点E,F(不与正方形的顶点重合),连接AE,EF,FA,使得∠EAF=45°.现拟将图中阴影部分规划为蜂源植物生长区,△AEF部分规划为蜂巢区,△CEF部分规划为蜂蜜交易区.若蜂源植物生长区的投入约为2×105元/百米2,蜂巢区与蜂蜜交易区的投入约为105元/百米2,则这三个区域的总投入最少需要多少元?
一位创业青年租用了一块边长为1百米的正方形田地ABCD来养蜂、产蜜与售蜜,他在正方形的边BC,CD上分别取点E,F(不与正方形的顶点重合),连接AE,EF,FA,使得∠EAF=45°.现拟将图中阴影部分规划为蜂源植物生长区,△AEF部分规划为蜂巢区,△CEF部分规划为蜂蜜交易区.若蜂源植物生长区的投入约为2×105元/百米2,蜂巢区与蜂蜜交易区的投入约为105元/百米2,则这三个区域的总投入最少需要多少元? 分析 方法一、设阴影部分面积为S,三个区域的总投入为T,可得T=2×105S+105(1-S)=105(S+1),设∠EAB=α(0°<α<45°),由解三角形可得S=$\frac{1}{2}$(tanα+$\frac{1-tanα}{1+tanα}$),令x=tanα∈(0,1),可得S=$\frac{1}{2}$(x-$\frac{x-1}{x+1}$),变形整理,运用基本不等式可得最小值;
方法二、设阴影部分面积为S,三个区域的总投入为T.设∠DAF=α,∠BAE=β(0°<α,β<45°),由解三角形可得S=$\frac{1}{2}$(tanα+tanβ),运用两角和的正切公式和基本不等式,即可得到所求最小值.
解答 解法一:设阴影部分面积为S,三个区域的总投入为T.
则T=2×105S+105(1-S)=105(S+1),
从而只要求S的最小值.
设∠EAB=α(0°<α<45°)
在△ABE中,因为AB=1,∠B=90°,
所以BE=tanα,
则S△ABE=$\frac{1}{2}$AB•BE=$\frac{1}{2}$tanα;
又∠DAF=45°-α,所以S△ADF=$\frac{1}{2}$tan(45°-α);
所以S=$\frac{1}{2}$(tanα+tan(45°-α))=$\frac{1}{2}$(tanα+$\frac{1-tanα}{1+tanα}$),
令x=tanα∈(0,1),
则S=$\frac{1}{2}$(x-$\frac{x-1}{x+1}$)=$\frac{1}{2}$[(x+1)+$\frac{2}{x+1}$-2]≥$\frac{1}{2}$(2$\sqrt{2}$-2)=$\sqrt{2}$-1.
当且仅当x+1=$\frac{2}{x+1}$,即x=$\sqrt{2}$-1时取等号,
从而三个区域的总投入T的最小值约为$\sqrt{2}$×105元.
(说明:这里S的最小值也可以用导数来求解).
因为S′=$\frac{(x+\sqrt{2}+1)(x-\sqrt{2}+1)}{2(1+x)^{2}}$,则由S′=0,得x=$\sqrt{2}$-1.
当x∈(0,$\sqrt{2}$-1)时,S′<0,S递减;当x∈($\sqrt{2}$-1,1)时,S′>0,S递增.
所以当x=$\sqrt{2}$-1时,S取得最小值为$\sqrt{2}$-1.
解法二:设阴影部分面积为S,三个区域的总投入为T.
则T=2×105S+105(1-S)=105(S+1),从而只要求S的最小值.
设∠DAF=α,∠BAE=β(0°<α,β<45°),则S=$\frac{1}{2}$(tanα+tanβ),
因为α+β=90°-∠EAF=45°,
所以tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=1,
所以tanα+tanβ=1-tanαtanβ≥1-($\frac{tanα+tanβ}{2}$)2,
即2S≥1-S2,解得S≥$\sqrt{2}$-1,即S取得最小值为$\sqrt{2}$-1,
从而三个区域的总投入T的最小值约为$\sqrt{2}$×105元.
点评 本题考查导数在实际问题中的运用:求最值,考查化简整理的运算能力,正确求出函数解析式和运用基本不等式或三角函数的恒等变换公式是解题的关键,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (-∞,-3] | C. | [-3,1] | D. | (-∞,-3]∪[1,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com