
分析 (1)求出函数的导数,得到关于a,b的方程组,解出a,b的值,从而求出函数的单调区间即可;
(2)根据f(x)的单调性,得到f($\frac{1}{e}$-1)>f(e-1),从而求出t的范围;
(3)问题转化为2ln(x+1)+x2-3x≤m在x∈(-1,2)上恒成立,令h(x)=2ln(x+1)+x2-3x,根据函数的单调性求出m的范围即可.
解答 解:(1)由题意得:x∈(-1,+∞),
f′(x)=$\frac{a}{x+1}$-2b(x+1),f′(1)=$\frac{a}{2}$-4b,f(1)=aln2-4b,
∴$\left\{\begin{array}{l}{\frac{a}{2}-4b=-3}\\{aln2-4b=2ln2-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{b=1}\end{array}\right.$,
∴f′(x)=$\frac{-2{(x}^{2}+2x)}{x+1}$,
∵x∈(-1,+∞),当x∈(-1,0)时,f′(x)>0,f(x)递增,
x∈(0,+∞)时,f′(x)<0,f(x)递减;
(2)由题意:t=2ln(x+1)-(x+1)2,
由(1)得:x∈($\frac{1}{e}$-1,0),f(x)递增,x∈(0,e-1),f(x)递减,
而f(0)=-1,f($\frac{1}{e}$-1)=-2-$\frac{1}{{e}^{2}}$,f(e-1)=2-e2,
∵-2-$\frac{1}{{e}^{2}}$-(2-e2)>0,
∴f($\frac{1}{e}$-1)>f(e-1),
要使方程f(x)-t=0在[${\frac{1}{e}$-1,e-1]内有两个不等实数根,
只需-2-$\frac{1}{{e}^{2}}$≤t<-1,
∴-2-$\frac{1}{{e}^{2}}$≤t<-1;
(3)由f(x)≤g(x)可得:2ln(x+1)-(x+1)2≤-2x2+x+m-1,
即2ln(x+1)+x2-3x≤m在x∈(-1,2)上恒成立,
令h(x)=2ln(x+1)+x2-3x,
h′(x)=$\frac{2}{x+1}$+2x-3=$\frac{(2x+1)(x-1)}{x+1}$,
令h′(x)>0,解得:x>1或x<-$\frac{1}{2}$,
令h′(x)<0,解得:-$\frac{1}{2}$<x<1,
∴h(x)在(-1,-$\frac{1}{2}$)递增,在(-$\frac{1}{2}$,1)递减,在(1,2)递增,
而h(-$\frac{1}{2}$)=$\frac{7}{4}$-2ln2,h(2)=2ln3-2,h(-$\frac{1}{2}$)-h(2)=$\frac{15}{4}$-2ln6>0,
∴h(x)max=h(-$\frac{1}{2}$)=$\frac{7}{4}$-ln2,
∴m≥$\frac{7}{4}$-ln2.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查转化思想以及切线方程,是一道综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| p(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
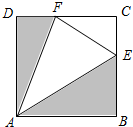 一位创业青年租用了一块边长为1百米的正方形田地ABCD来养蜂、产蜜与售蜜,他在正方形的边BC,CD上分别取点E,F(不与正方形的顶点重合),连接AE,EF,FA,使得∠EAF=45°.现拟将图中阴影部分规划为蜂源植物生长区,△AEF部分规划为蜂巢区,△CEF部分规划为蜂蜜交易区.若蜂源植物生长区的投入约为2×105元/百米2,蜂巢区与蜂蜜交易区的投入约为105元/百米2,则这三个区域的总投入最少需要多少元?
一位创业青年租用了一块边长为1百米的正方形田地ABCD来养蜂、产蜜与售蜜,他在正方形的边BC,CD上分别取点E,F(不与正方形的顶点重合),连接AE,EF,FA,使得∠EAF=45°.现拟将图中阴影部分规划为蜂源植物生长区,△AEF部分规划为蜂巢区,△CEF部分规划为蜂蜜交易区.若蜂源植物生长区的投入约为2×105元/百米2,蜂巢区与蜂蜜交易区的投入约为105元/百米2,则这三个区域的总投入最少需要多少元?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 100 |
| p(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com