
分析 (1)利用绝对值的意义,求函数y=f(x)的最小值;
(2)由题意可得|x-1|+|x-2|小于或等于$\frac{|a+b|+|a-b|}{|a|}$的最小值,而$\frac{|a+b|+|a-b|}{|a|}$的最小值等于2,故x的范围即为不等式|x-1|+|x-2|≤2的解,根据数轴上的$\frac{1}{2}$、$\frac{5}{2}$对应点到1和2对应点的距离之和等于2,可得不等式的解集.
解答 解:(1)x≥2,f(x)≥1;
1<x<2,f(x)=1;
x≤1,f(x)=3-2x≥1,
∴函数y=f(x)的最小值为1;
(2)解:由题知,|x-1|+|x-2|≤$\frac{|a+b|+|a-b|}{|a|}$恒成立,
故|x-1|+|x-2|小于或等于 $\frac{|a+b|+|a-b|}{|a|}$的最小值.
∵|a+b|+|a-b|≥|a+b+a-b|=2|a|,当且仅当 (a+b)(a-b)≥0 时取等号,
∴$\frac{|a+b|+|a-b|}{|a|}$的最小值等于2,
∴x的范围即为不等式|x-1|+|x-2|≤2的解.
由于|x-1|+|x-2|表示数轴上的x对应点到1和2对应点的距离之和,
又由于数轴上的$\frac{1}{2}$、$\frac{5}{2}$对应点到1和2对应点的距离之和等于2,
故不等式的解集为[$\frac{1}{2}$,$\frac{5}{2}$].
点评 本题考查绝对值的意义,绝对值不等式的解法,判断|x-1|+|x-2|表示数轴上的x对应点到1和2对应点的距离之和,是解题的关键.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
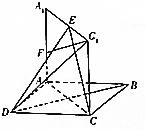 如图所示,四边形ABCD为菱形,矩形A1ACC1⊥平面ABCD,且DA=2,AA1=3,∠ADC=$\frac{π}{3}$,E为线段A1C1的中点,F为线段A1A上一点.
如图所示,四边形ABCD为菱形,矩形A1ACC1⊥平面ABCD,且DA=2,AA1=3,∠ADC=$\frac{π}{3}$,E为线段A1C1的中点,F为线段A1A上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
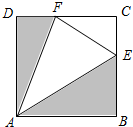 一位创业青年租用了一块边长为1百米的正方形田地ABCD来养蜂、产蜜与售蜜,他在正方形的边BC,CD上分别取点E,F(不与正方形的顶点重合),连接AE,EF,FA,使得∠EAF=45°.现拟将图中阴影部分规划为蜂源植物生长区,△AEF部分规划为蜂巢区,△CEF部分规划为蜂蜜交易区.若蜂源植物生长区的投入约为2×105元/百米2,蜂巢区与蜂蜜交易区的投入约为105元/百米2,则这三个区域的总投入最少需要多少元?
一位创业青年租用了一块边长为1百米的正方形田地ABCD来养蜂、产蜜与售蜜,他在正方形的边BC,CD上分别取点E,F(不与正方形的顶点重合),连接AE,EF,FA,使得∠EAF=45°.现拟将图中阴影部分规划为蜂源植物生长区,△AEF部分规划为蜂巢区,△CEF部分规划为蜂蜜交易区.若蜂源植物生长区的投入约为2×105元/百米2,蜂巢区与蜂蜜交易区的投入约为105元/百米2,则这三个区域的总投入最少需要多少元?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,1] | B. | (-3,3) | C. | (-3,-1]∪[1,3) | D. | (-3,-1)∪(1,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com