
分析 把已知关于x的方程变形,利用△≥0配方得到(lga-lgb)2≥4,进一步得到$lg\frac{a}{b}≤-2$或$lg\frac{a}{b}≥2$,从而求得$\frac{a}{b}$的取值范围.
解答 解:由lg(ax)•lg(bx)+1=0,得(lga+lgx)(lgb+lgx)+1=0.
即lg2x+(lga+lgb)lgx+lgalgb+1=0.
由△=(lga+lgb)2-4lgalgb-4=(lga-lgb)2-4≥0,
得$lg\frac{a}{b}≤-2$或$lg\frac{a}{b}≥2$,
∴0$<\frac{a}{b}≤\frac{1}{100}$或$\frac{a}{b}≥100$.
∴$\frac{a}{b}$的取值范围是(0,$\frac{1}{100}$]∪[100,+∞).
故答案为:(0,$\frac{1}{100}$]∪[100,+∞).
点评 本题考查基本不等式的应用,考查对数运算性质,体现了数学转化思想方法,属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4.
如图,BD为⊙O的直径,AB=AC,AD交BC于E,AE=2,ED=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
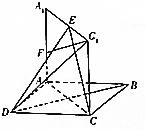 如图所示,四边形ABCD为菱形,矩形A1ACC1⊥平面ABCD,且DA=2,AA1=3,∠ADC=$\frac{π}{3}$,E为线段A1C1的中点,F为线段A1A上一点.
如图所示,四边形ABCD为菱形,矩形A1ACC1⊥平面ABCD,且DA=2,AA1=3,∠ADC=$\frac{π}{3}$,E为线段A1C1的中点,F为线段A1A上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
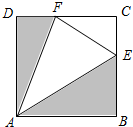 一位创业青年租用了一块边长为1百米的正方形田地ABCD来养蜂、产蜜与售蜜,他在正方形的边BC,CD上分别取点E,F(不与正方形的顶点重合),连接AE,EF,FA,使得∠EAF=45°.现拟将图中阴影部分规划为蜂源植物生长区,△AEF部分规划为蜂巢区,△CEF部分规划为蜂蜜交易区.若蜂源植物生长区的投入约为2×105元/百米2,蜂巢区与蜂蜜交易区的投入约为105元/百米2,则这三个区域的总投入最少需要多少元?
一位创业青年租用了一块边长为1百米的正方形田地ABCD来养蜂、产蜜与售蜜,他在正方形的边BC,CD上分别取点E,F(不与正方形的顶点重合),连接AE,EF,FA,使得∠EAF=45°.现拟将图中阴影部分规划为蜂源植物生长区,△AEF部分规划为蜂巢区,△CEF部分规划为蜂蜜交易区.若蜂源植物生长区的投入约为2×105元/百米2,蜂巢区与蜂蜜交易区的投入约为105元/百米2,则这三个区域的总投入最少需要多少元?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com