已知数列{an}的前n项和为Sn,点(n,Sn)(n∈N+)在函数f(x)=32x-x2+1的图象上,
(1)求数列{an}的通项公式;
(2)求数列{an}的前多少项和最大.
【答案】
分析:(1)当n=1时,a
1=S
1,n≥2时,a
n=S
n-S
n-1即可得出a
n.
(2)解出a
n>0即可得出.
解答:解:(1)∵点(n,S
n)(n∈N
+)在函数f(x)=32x-x
2+1的图象上,∴
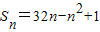
.
∴当n=1时,a
1=S
1=32-1+1=32.
n≥2时,a
n=S
n-S
n-1=32n-n
2+1-[32(n-1)-(n-1)
2+1]=33-2n.
当n=1时,上式不成立.
∴数列{a
n}的通项公式为
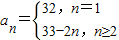
;
(2)由a
n=33-2n≥0,解得n
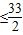
=16+

.a
1>0.
∴数列{a
n}的前16项和最大.
点评:熟练掌握“当n=1时,a
1=S
1,n≥2时,a
n=S
n-S
n-1即可得出a
n”及其前n项和最大与通项公式的关系等是解题的关键.

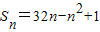 .
.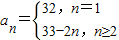 ;
;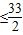 =16+
=16+ .a1>0.
.a1>0.
