
分析 (1)由二项式系数即为该项的系数,再由二项式系数的性质,即可得到;
(2)由展开式中的通项,得到各项的二项式系数,再由等比数列的性质,结合组合数公式,化简整理,解方程即可求出n;
(3)写出通项,化简整理,判断r是6的倍数,又0≤r≤14,列举出所有的有理项即可.
解答 解:(1)二项式展开式中各项系数之和就是二项式展开式中各项的二项式系数之和
∴二项式展开式中各项系数之和为${C}_{n}^{0}+{C}_{n}^{1}+{C}_{n}^{2}$+…+${C}_{n}^{n}$=2n,
(2)展开式中第9项,第10项,第11项的二项式系数分别是Cn8,Cn9,Cn10,依题意得Cn8+Cn10=2Cn9,
写成$\frac{n!}{8!(n-8)!}$+$\frac{n!}{10!(n-10)!}$=2•$\frac{n!}{9!(n-9)!}$
化简得90+(n-9)(n-8)=2•10(n-8),
即:n2-37n+322=0,解得n=14或n=23;
(3)展开式的通项为Tr+1=${C}_{14}^{r}$${x}^{\frac{14-r}{2}}$•${x}^{\frac{r}{3}}$=${C}_{14}^{r}{x}^{\frac{42-r}{6}}$,
∴展开式中的有理项当且仅当r是6的倍数,又0≤r≤14,
∴展开式中的有理项共3项是r=0,r=6,r=12,
∴展开式中的有理项是T1=${C}_{14}^{0}$x7=x7,T7=${C}_{14}^{6}$x6=3003x6,T13=${C}_{14}^{12}$x5=91x5.
点评 本题主要考查二项式定理的运用,注意运用通项公式求某一项,区别二项式系数与某一项的系数,注意隐含条件的运用,考查组合数的公式及指数的运算,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | ac>bc | C. | $\sqrt{a}$>$\sqrt{b}$ | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
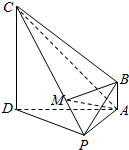 在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).
在四棱锥P-ABCD中,CD⊥平面PAD,AB∥CD,AD⊥PA,△ADC、△PAD均为等腰三角形,AD=4AB=4,M为线段CP上一点,且$\overrightarrow{PM}$=λ$\overrightarrow{PC}$(0≤λ≤1).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com