
分析 由已知得$\overrightarrow{B{D}_{1}}$=$\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{D{D}_{1}}$,由此能求出点B与点D1两点间的距离.
解答  解:∵四棱柱ABCD-A1B1C1D1各棱长均为1,∠A1AB=∠A1AD=∠BAD=60°,
解:∵四棱柱ABCD-A1B1C1D1各棱长均为1,∠A1AB=∠A1AD=∠BAD=60°,
∴$\overrightarrow{B{D}_{1}}$=$\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{D{D}_{1}}$,
∴${\overrightarrow{B{D}_{1}}}^{2}$=($\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{D{D}_{1}}$)2=${\overrightarrow{BA}}^{2}+{\overrightarrow{AD}}^{2}+{\overrightarrow{D{D}_{1}}}^{2}$+2$\overrightarrow{BA}•\overrightarrow{AD}$+2$\overrightarrow{BA}•\overrightarrow{D{D}_{1}}$+2$\overrightarrow{AD}•\overrightarrow{D{D}_{1}}$
=1+1+1+2×1×1×cos120°+2×1×1×cos120°+2×1×1×cos60°
=2,
∴|$\overrightarrow{B{D}_{1}}$|=$\sqrt{2}$.
∴点B与点D1两点间的距离为$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查两点间距离的求法,是基础题,解题时要认真审题,注意向量法的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
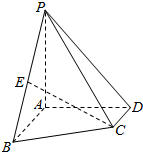 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,AB=AD=2CD,E为PB的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,AB=AD=2CD,E为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 5$\sqrt{2}$ | C. | 5 | D. | 4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com