
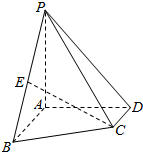
 如图,四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,AB=AD=2CD,E为PB的中点.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,AB∥CD,∠BAD=∠ADC=90°,AB=AD=2CD,E为PB的中点.分析 (1)取AB中点F,连结EF、FC,则EF∥PA,CF∥AD,从而EF⊥AB,AB⊥CF,由此能证明CE⊥AB.
(2)推导出PA⊥CD,CD⊥PD,则∠PDA为二面角P-CD-A的平面角,由此能求出直线CE与平面PAB所成角的正切值.
(3)过P作PG∥CD,推导出∠APD为所求锐二面角的平面角,由此能求出平面PCD与平面PAB所成的锐二面角的余弦值.
解答 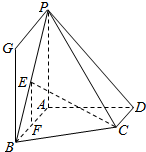 证明:(1)取AB中点F,连结EF、FC,则EF∥PA,CF∥AD,
证明:(1)取AB中点F,连结EF、FC,则EF∥PA,CF∥AD,
∵PA⊥平面ABCD,∴EF⊥平面ABCD,
∵AB?平面ABCD,∴EF⊥AB,
∵AB⊥AD,∴AB⊥CF,
∵EF?平面EFC,CF?平面EFC,∴AB⊥平面EFC,
∵CE?平面EFC,∴CE⊥AB.
解:(2)∵PA⊥平面ABCD,CD?平面ABCD,∴PA⊥CD,
∵AD⊥CD,∴CD⊥平面PAD,∴CD⊥PD,
∴∠PDA为二面角P-CD-A的平面角,
∴∠PDA=60°,∴PA=$\sqrt{3}AD$,
∵AB=AD=2CD,∴PA=$\sqrt{3}AB$=$\sqrt{3}AD$,
由(1)知,∠CEF为CE于平面PAB所成角,
∵tan∠CEF=$\frac{CF}{EF}$=$\frac{AD}{EF}$=$\frac{2}{\frac{1}{2}•2\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$,
∴直线CE与平面PAB所成角的正切值为$\frac{2\sqrt{3}}{3}$.
(3)过P作PG∥CD,由PA⊥平面PAD,得PA⊥AB,PA⊥PG,
由BA⊥平面PAD,得CD⊥平面PAD,
∴CD⊥PD,PG⊥PD,
∴∠APD为所求锐二面角的平面角,
cos$∠APD=\frac{PA}{PD}$=$\frac{1}{\sqrt{1+{k}^{2}}}$.
点评 本题考查异面直线垂直的证明,考查线面角的正切值的求法,考查二面角的平面角的余弦值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:选择题
| A. | [2,5] | B. | (2,5] | C. | [-1,2] | D. | [-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | ac>bc | C. | $\sqrt{a}$>$\sqrt{b}$ | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{a}$>$\frac{1}{b}$ | B. | ac>bc | C. | $\sqrt{a}$>$\sqrt{b}$ | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p | B. | p∧q | C. | ¬p∨q | D. | ¬p∨¬q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com