
已知函数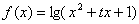 (
(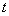 为常数,且
为常数,且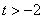 ).
).
(1)当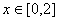 时,求函数
时,求函数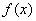 的最小值(用
的最小值(用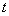 表示);
表示);
(2)是否存在不同的实数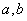 使得
使得 ,
,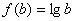 ,并且
,并且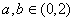 ,若存在,求出实数
,若存在,求出实数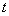 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
科目:高中数学 来源: 题型:
已知函数f(x)=loga(1﹣x)+loga(x+3),其中0<a<1,记函数f(x)的定义域为D.
(1)求函数f(x)的定义域D;
(2)若函数f(x)的最小值为﹣4,求a的值;
(3)若对于D内的任意实数x,不等式﹣x2+2mx﹣m2+2m<1恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合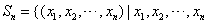 是正整数
是正整数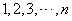 的一个排列
的一个排列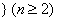 ,函数
,函数
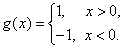
对于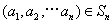 ,定义:
,定义: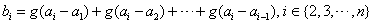 ,
,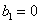 ,称
,称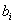 为
为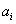 的满意指数.排列
的满意指数.排列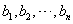 为排列
为排列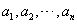 的生成列.
的生成列.
(Ⅰ)当 时,写出排列
时,写出排列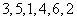 的生成列;
的生成列;
(Ⅱ)证明:若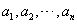 和
和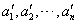 为
为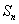 中两个不同排列,则它们的生成列也不同;
中两个不同排列,则它们的生成列也不同;
(Ⅲ)对于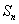 中的排列
中的排列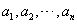 ,进行如下操作:将排列
,进行如下操作:将排列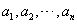 从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加
从左至右第一个满意指数为负数的项调至首项,其它各项顺序不变,得到一个新的排列.证明:新的排列的各项满意指数之和比原排列的各项满意指数之和至少增加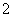 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
下列说法中正确的是:
①函数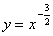 的定义域是
的定义域是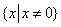 ;
;
②方程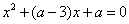 有一个正实根,一个负实根,则
有一个正实根,一个负实根,则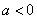 ;
;
③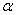 是第二象限角,
是第二象限角,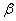 是第一象限角,则
是第一象限角,则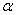 >
>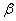 ;
;
④函数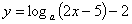 ,
,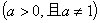 恒过定点(3,-2);
恒过定点(3,-2);
⑤若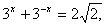 则
则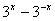 的值为2
的值为2
⑥若定义在R上的函数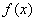 满足:对任意
满足:对任意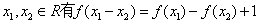 ,则
,则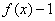 为奇函数
为奇函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com