
分析 化简($\frac{27}{8}$)${\;}^{-\frac{1}{3}}$=$((\frac{3}{2})^{3})^{-\frac{1}{3}}$=$\frac{2}{3}$,cosπ=-1,log2$\root{3}{4}$=$\frac{2}{3}$,${C}_{9}^{7}$=$\frac{9×8}{2×1}$=36,从而求得.
解答 解:∵($\frac{27}{8}$)${\;}^{-\frac{1}{3}}$=$((\frac{3}{2})^{3})^{-\frac{1}{3}}$=$\frac{2}{3}$,cosπ=-1,
log2$\root{3}{4}$=$\frac{2}{3}$,${C}_{9}^{7}$=$\frac{9×8}{2×1}$=36,
∴($\frac{27}{8}$)${\;}^{-\frac{1}{3}}$-cosπ-log2$\root{3}{4}$+${C}_{9}^{7}$=37,
故答案为:37.
点评 本题考查了对数运算与指数运算的应用,属于基础题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -10 | B. | $\frac{1}{10}$ | C. | 10 | D. | 20 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:选择题
如图, 两点在反比例函数
两点在反比例函数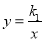 的图象上,
的图象上, 两点在反比例函数
两点在反比例函数 的图象上,
的图象上,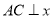 轴于点
轴于点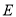 ,
, 轴于点
轴于点 ,
,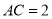 ,
, ,
, ,则
,则 =( )
=( )

A.4 B.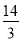 C.
C. D.6[
D.6[
查看答案和解析>>
科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(文)试卷(解析版) 题型:选择题
如图,在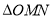 中,
中,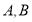 分别是
分别是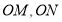 的中点,若
的中点,若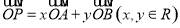 ,且点
,且点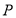 落在四边形
落在四边形 内(含边界),则
内(含边界),则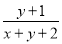 的取值范围是( )
的取值范围是( )

A.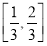 B.
B.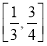 C.
C. D.
D.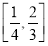
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com