
分析 展开式的x项来源于第一个括号的1和m=(x+$\frac{2}{x}$)5展开式的x项的乘积或第一个括号的2x和m=(x+$\frac{2}{x}$)5展开式的常数项的乘积,分别由m的展开式可得.
解答 解:展开式的x项来源于第一个括号的1和m=(x+$\frac{2}{x}$)5展开式的x项的乘积
或第一个括号的2x和m=(x+$\frac{2}{x}$)5展开式的常数项的乘积,
又m=(x+$\frac{2}{x}$)5的通项为Tk+1=${C}_{5}^{k}$x5-k($\frac{2}{x}$)k=2k•${C}_{5}^{k}$x5-2k,
令5-2k=1可得k=2,故m展开式中含x的项为40x,
令5-2k=0可得k=$\frac{5}{2}$∉Z,故m展开式中无常数项,
∴原式展开式中x的系数为40,
故答案为:40.
点评 本题考查二项式定理和二项式系数,分类讨论是解决问题的关键,属基础题.


科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,-1) | C. | (-1,0) | D. | (1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
查看答案和解析>>
科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(文)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知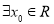 使不等式
使不等式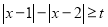 成立.
成立.
(1)求满足条件的实数 的集合
的集合 ;
;
(2)若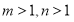 ,对
,对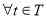 ,不等式
,不等式 恒成立,求
恒成立,求 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com