
分析 (1)通过在Tn=(2n-3)•2n+3中分别令n=1、2、3,可得数列{cn}的前三项的值,利用公差和公比分别表示,计算可知d=q=2,进而计算可得结论;
(2)通过假设存在满足条件的p、q∈N*,代入化简可知(p-$2\frac{q-2}{2}$)(p+$2\frac{q-2}{2}$)=1008,通过分析可知$2\frac{q-2}{2}$只能取1,2,22,…,29,进而筛选可确定p、q的值.
解答 解:(1)∵Tn=(2n-3)•2n+3,
∴T1=a1b1=1,a2b2=T2-T1=6,a3b3=T3-T2=20,
∴(1+d)q=6,(1+2d)q2=20,
整理得:$\frac{36}{(1+d)^{2}}$=q2=$\frac{20}{1+2d}$,
解得:d=2或d=-$\frac{2}{5}$(舍),
从而q=$\frac{6}{1+2}$=2,
∴an=1+2(n-1)=2n-1,
bn=1•2n-1=2n-1;
(2)结论:存在p=32、q=6,使得$\frac{1}{2}$(ap+1)2-bq=2016成立.
理由如下:
假设存在p,q∈N*,使得$\frac{1}{2}$(ap+1)2-bq=2016成立,
则$\frac{1}{2}$(2p-1+1)2-2q-1=2016,即2p2-2q-1=2016,
∴p2-2q-2=1008,即(p-$2\frac{q-2}{2}$)(p+$2\frac{q-2}{2}$)=1008,
又∵p,q∈N*,
∴$2\frac{q-2}{2}$只能取1,2,22,…,29,
∴2q-2只能取1,4,42,…,49,
又∵p2=2q-2+42×63,
∴只有42+42×63为平方数,
此时,q=6,p=32.
点评 本题考查数列的通项,考查数列的递推式,注意解题方法的积累,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 集合M中共有2个元素 | B. | 集合M中共有2个相同元素 | ||
| C. | 集合M中共有1个元素 | D. | 集合M为空集 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年山西忻州一中高一上学期新生摸底数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点 ,
, ,
, ,
, ,
, ,
, ,…,则点
,…,则点 的坐标是 .
的坐标是 .

查看答案和解析>>
科目:高中数学 来源:2017届河北衡水中学高三上学期调研三考数学(文)试卷(解析版) 题型:解答题
设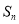 为各项不相等的等差数列
为各项不相等的等差数列 的前
的前 项和,已知
项和,已知 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 为数列
为数列 的前
的前 项和,求
项和,求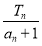 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com