
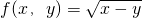 �� ��f��x��y��=x2+y2��
�� ��f��x��y��=x2+y2�� =
= -y=1����ʱ�У�x-y��2=4��������x-
-y=1����ʱ�У�x-y��2=4��������x- ��2=��
��2=�� -y��2=1����f��x��y����f��x��z��+f��z��y�������������Բ��������Dz���ʽ��
-y��2=1����f��x��y����f��x��z��+f��z��y�������������Բ��������Dz���ʽ�� �����壬�ʢ۲��ԣ�
�����壬�ʢ۲��ԣ�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| x-y |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���ӱ�ʡ������ѧ2011�����4��ģ�⿼����ѧ�������� ���ͣ�013
��֪����(y��1)(|x|��2)��4�����������x��[a��b](a��b��Z)��������Ψһ��y��[0��1]ʹ���̶��������Ҷ�����y��[0��1]������x��[a��b](a��b��Z)ʹ���̳�������a��b�����ֵ����
0
2
4
6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ���ѡ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡģ���� ���ͣ������
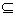 R��B
R��B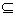 R)����Ψһȷ����f(x��y)��֮��Ӧ�����f(x��y)Ϊ����x��y�Ķ�Ԫ������
R)����Ψһȷ����f(x��y)��֮��Ӧ�����f(x��y)Ϊ����x��y�Ķ�Ԫ������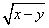 ����f(x��y)=x2+y2��
����f(x��y)=x2+y2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com