
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() .四边形
.四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
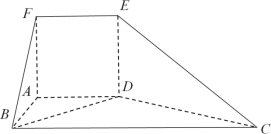
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() 若存在,求
若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)详见解析;(Ⅱ)![]() ;(Ⅲ)线段
;(Ⅲ)线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.
【解析】
(I)根据面面垂直的性质定理,证得![]() 平面
平面![]() ,由此证得
,由此证得![]() .(II)以
.(II)以![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,通过计算直线
轴建立空间直角坐标系,通过计算直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,由此计算出线面角的正弦值.(III)设
的法向量,由此计算出线面角的正弦值.(III)设![]() ,用
,用![]() 表示出
表示出![]() 点的坐标,利用直线
点的坐标,利用直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量垂直列方程,解方程求得
的法向量垂直列方程,解方程求得![]() 的值,由此判断存在符合题意的点
的值,由此判断存在符合题意的点![]() .
.
解:(Ⅰ)证明:因为![]() 为正方形,
为正方形,
所以![]() .
.
又因为平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
所以![]() .
.
(Ⅱ)由(Ⅰ)可知,![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() 两两垂直.
两两垂直.
分别以![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系(如图).
轴建立空间直角坐标系(如图).
因为![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则 即
即![]()
令![]() ,则
,则![]() ,
,
所以![]() .
.
设直线与平面
![]() 所成角为
所成角为![]() ,
,
则![]() .
.
(Ⅲ)设![]() ,
,
设![]() ,则
,则![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则
因为![]() ,所以
,所以![]()
令![]() ,则
,则![]() ,所以
,所以![]() .
.
在线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() 等价于存在
等价于存在![]() ,使得
,使得![]() .
.
因为![]() ,由
,由![]() ,
,
所以![]() ,
,
![]() ,
,
所以线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ,且
,且![]() .
.



 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知直线![]() 的方程为
的方程为![]() ,
,![]() .
.
(1)若直线![]() 在
在![]() 轴、
轴、![]() 轴上的截距之和为-1,求坐标原点
轴上的截距之和为-1,求坐标原点![]() 到直线
到直线![]() 的距离;
的距离;
(2)若直线![]() 与直线
与直线![]() :
:![]() 和
和![]() :
:![]() 分别相交于
分别相交于![]() 、
、![]() 两点,点
两点,点![]() 到
到![]() 、
、![]() 两点的距离相等,求
两点的距离相等,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
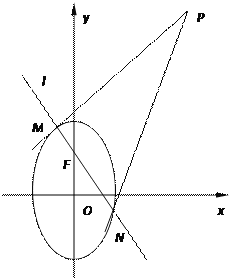
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,且上焦点为
,且上焦点为![]() ,过
,过![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点.设点
两点.设点![]() ,记
,记![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 和
和![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)如果直线![]() 的斜率等于
的斜率等于![]() ,求
,求![]() 的值;
的值;
(3)探索![]() 是否为定值?如果是,求出该定值;如果不是,求出
是否为定值?如果是,求出该定值;如果不是,求出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】天坛公园是明、清两代皇帝“祭天”“祈谷”的场所.天坛公园中的圜丘台共有三层(如图1所示),上层坛的中心是一块呈圆形的大理石板,从中心向外围以扇面形石(如图2所示).上层坛从第一环至第九环共有九环,中层坛从第十环至第十八环共有九环,下层坛从第十九环至第二十七环共有九环;第一环的扇面形石有9块,从第二环起,每环的扇面形石块数比前一环多9块,则第二十七环的扇面形石块数是______;上、中、下三层坛所有的扇面形石块数是_______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,ABCD为矩形,点A、E、B、F共面,且![]() 和
和![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() 90°.
90°.

(Ⅰ)若平面ABCD![]() 平面AEBF,证明平面BCF
平面AEBF,证明平面BCF![]() 平面ADF;
平面ADF;
(Ⅱ)问在线段EC上是否存在一点G,使得BG∥平面CDF,若存在,求出此时三棱锥G-ABE与三棱锥G-ADF的体积之比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四种说法中正确的有______.(填序号)①数据2,2,3,3,4,6,7,3的众数与中位数相等;②数据1,3,5,7,9的方差是数据2,6,10,14,18的方差的一半;③一组数据的方差大小反映该组数据的波动性,若方差越大,则波动性越大,方差越小,则波动性越小.④频率分布直方图中各小长方形的面积等于相应各组的频数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率
,离心率![]() ,点
,点![]() 是椭圆上的一个动点,
是椭圆上的一个动点,![]() 面积的最大值是
面积的最大值是![]() .
.
(1)求椭圆的方程;
(2)已知点![]() ,问是否存在直线
,问是否存在直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() ,若存在,求出直线
,若存在,求出直线![]() 斜率的取值范围;若不存在,说明理由.
斜率的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com