
【题目】已知球O为三棱锥S﹣ABC的外接球,![]()
![]() ,则球O的表面积是( )
,则球O的表面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
根据题意能够求出弦![]() 的中垂面,那么中垂面一定经过球心,设出球心O位置,作
的中垂面,那么中垂面一定经过球心,设出球心O位置,作![]() ⊥平面SAC,可得
⊥平面SAC,可得![]() 为等边三角形SAC的中心,在三角形ABM中求球的半径,需要用到四点共圆的性质解题.
为等边三角形SAC的中心,在三角形ABM中求球的半径,需要用到四点共圆的性质解题.
解:取SC中点M,连接AM、MB,
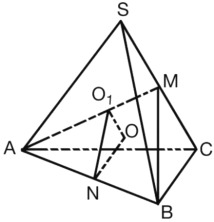
因为△SAC是等边三角形,且SB=BC,
∴AM⊥SC,MB⊥SC,
∴SC⊥平面AMB,
∴球心O在平面AMB上,作![]() ⊥平面SAC,可得
⊥平面SAC,可得![]() 为等边三角形SAC的中心,
为等边三角形SAC的中心,
所以![]() =
=![]() ,
,
取AB中点N,连接ON,∴ON⊥AB,
∴![]() 四点共圆,AO为这四点共圆的直径,也是三棱锥SABC外接球的半径,连接
四点共圆,AO为这四点共圆的直径,也是三棱锥SABC外接球的半径,连接![]() ,
,
在△ABM中:![]() ,
,
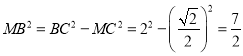 ,
,
![]()
∴∠MAB=90°,
∴在直角三角形![]() 中,
中,
由勾股定理,得![]() =
=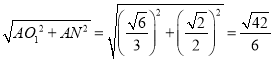 ,
,
∴三棱锥SABC外接球的半径长为AO=![]() =
=![]() ,
,![]() .
.
故选:A.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
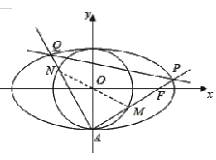
【题目】在平面直角坐标系![]() 中,设椭圆
中,设椭圆![]() 的下顶点为
的下顶点为![]() ,右焦点为
,右焦点为![]() ,离心率为
,离心率为![]() .已知点
.已知点![]() 是椭圆上一点,当直线
是椭圆上一点,当直线![]() 经过点
经过点![]() 时,原点
时,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与圆
与圆![]() :相交于点
:相交于点![]() (异于点
(异于点![]() ),设点
),设点![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,直线
,直线![]() 与椭圆相交于点
与椭圆相交于点![]() (异于点
(异于点![]() ).①若
).①若![]() ,求
,求![]() 的面积;②设直线
的面积;②设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,求证:
,求证:![]() 是定值.
是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三家企业产品的成本分别为10000,12000,15000,其成本构成如下图所示,则关于这三家企业下列说法错误的是( )
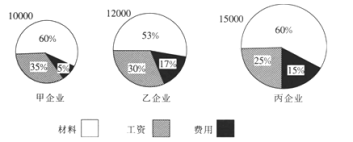
A.成本最大的企业是丙企业B.费用支出最高的企业是丙企业
C.支付工资最少的企业是乙企业D.材料成本最高的企业是丙企业
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 左顶点为M,上顶点为N,直线MN的斜率为
左顶点为M,上顶点为N,直线MN的斜率为![]() .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)直线l:![]() 与椭圆交于A,C两点,与y轴交于点P,以线段AC为对角线作正方形ABCD,若
与椭圆交于A,C两点,与y轴交于点P,以线段AC为对角线作正方形ABCD,若![]() .
.
(![]() )求椭圆方程;
)求椭圆方程;
(![]() )若点E在直线MN上,且满足
)若点E在直线MN上,且满足![]() ,求使得
,求使得![]() 最长时,直线AC的方程.
最长时,直线AC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个三角形数表按如下方式构成(如图:其中项数![]() ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:![]() ;
;![]() 为数表中第
为数表中第![]() 行的第
行的第![]() 个数.
个数.
![]()
![]() …
…![]()
![]()
![]()
![]() …
…![]()
![]() …
…![]()
……
![]()
(1)求第2行和第3行的通项公式![]() 和
和![]() ;
;
(2)证明:数表中除最后2行外每一行的数都依次成等差数列,并求![]() 关于
关于![]() 的表达式;
的表达式;
(3)若![]() ,
,![]() ,试求一个等比数列
,试求一个等比数列![]() ,使得
,使得![]() ,且对于任意的
,且对于任意的![]() ,均存在实数
,均存在实数![]() ,当
,当![]() 时,都有
时,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
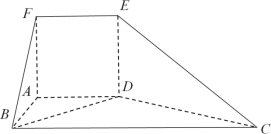
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() .四边形
.四边形![]() 为正方形,四边形
为正方形,四边形![]() 为梯形,且
为梯形,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() 若存在,求
若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为椭圆
为椭圆![]() 上任意一点,直线
上任意一点,直线![]() 与圆
与圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 的左焦点.
的左焦点.
(Ⅰ)求椭圆![]() 的离心率及左焦点
的离心率及左焦点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 与椭圆
与椭圆![]() 相切;
相切;
(Ⅲ)判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x),且对任意实数x都有f(x+2)=f(x),当x∈[0,1]时,f(x)=x2,若在区间[﹣3,3]内,函数g(x)=f(x)﹣kx﹣3k有6个零点,则实数k的取值范围为__.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com