
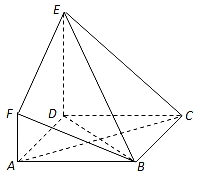
 如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.分析 (Ⅰ)推导出AC⊥BD,AC⊥DE,由此能证明AC⊥平面BDE.
(Ⅱ)该几何体的体积V=VB-AEF+VE-ABCD,由此能求出该几何体的体积.
解答 证明:(Ⅰ)∵ABCD是边长为3的正方形,∴AC⊥BD,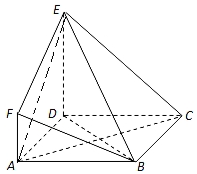
∵DE⊥平面ABCD,AC?平面ABCD,
∴AC⊥DE,
∵BD∩DE=D,∴AC⊥平面BDE.
解:(Ⅱ)∵ABCD是边长为3的正方形,AF∥DE,DE=3AF,
BE与平面ABCD所成角为60°.
∴BD=$\sqrt{9+9}$=3$\sqrt{2}$,ED=3$\sqrt{6}$,AF=$\sqrt{6}$,
由题意得DE⊥平面ABCD,AB⊥平面AEF,
∴该几何体的体积:
V=VB-AEF+VE-ABCD
=$\frac{1}{3}×3×[\frac{1}{2}(\sqrt{6}+3\sqrt{6})×3-\frac{1}{2}×3×3\sqrt{6}]$+$\frac{1}{3}×3\sqrt{6}×{3}^{2}$
=$\frac{21\sqrt{6}}{2}$.
点评 本题考查线面垂直的证明,考查几何体的体积的求法,涉及到空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想,是中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
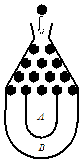 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中它将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中它将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某特色餐馆开通了美团外卖服务,在一周内的某特色外卖份数x(份)与收入y(元)之间有如下的对应数据:
某特色餐馆开通了美团外卖服务,在一周内的某特色外卖份数x(份)与收入y(元)之间有如下的对应数据:| 外卖份数x(份) | 2 | 4 | 5 | 6 | 8 |
| 收入y(元) | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
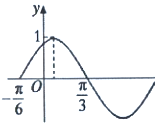 函数$f(x)=Asin({ωx+φ})({x∈R,A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,如果${x_1},{x_2}∈({-\frac{π}{6},\frac{π}{3}})$,且f(x1)=f(x2),则f(x1+x2)=( )
函数$f(x)=Asin({ωx+φ})({x∈R,A>0,ω>0,|φ|<\frac{π}{2}})$的部分图象如图所示,如果${x_1},{x_2}∈({-\frac{π}{6},\frac{π}{3}})$,且f(x1)=f(x2),则f(x1+x2)=( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com