
已知函数 (
(
 )
)
(1)若 从集合
从集合 中任取一个元素,
中任取一个元素, 从集合
从集合 中任取一个元素,
中任取一个元素,
求方程 恰有两个不相等实根的概率;
恰有两个不相等实根的概率;
(2)若 从区间
从区间 中任取一个数,
中任取一个数, 从区间
从区间 中任取一个数
中任取一个数
求方程 没有实根的概率.
没有实根的概率.
(1)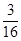 (2)
(2)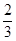
【解析】
试题分析:(1) ∵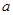 取集合
取集合 中任一个元素,
中任一个元素,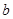 取集合{0,1,2,3}中任一个元素
取集合{0,1,2,3}中任一个元素
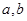 取值的情况是:
取值的情况是:
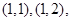
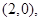
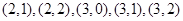 ,(0,3),(1,3),(2,3),(3,3)其中第一个数表示
,(0,3),(1,3),(2,3),(3,3)其中第一个数表示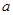 的取值,第二个数表示
的取值,第二个数表示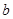 的取值.
的取值.
即基本事件总数为16 2分
设“方程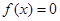 恰有两个不相等的实根”为事件
恰有两个不相等的实根”为事件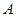 3分
3分
当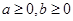 时,方程
时,方程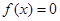 恰有两个不相等实根的充要条件为b>
恰有两个不相等实根的充要条件为b>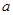 且
且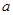 不等于零
不等于零
当b>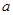 时,
时,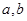 取值的情况有(1,2),(1,3),(2,3),
取值的情况有(1,2),(1,3),(2,3),
即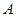 包含的基本事件数为3, 5分
包含的基本事件数为3, 5分
∴方程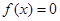 恰有两个不相等实根的概率
恰有两个不相等实根的概率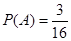 7分
7分
(2)∵若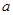 从区间
从区间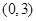 中任取一个数,
中任取一个数,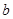 从区间
从区间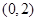 中任取一个数
中任取一个数
则试验的全部结果构成区域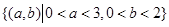
这是一个矩形区域,其面积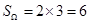 9分
9分
设“方程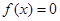 没有实根”为事件B, 10分
没有实根”为事件B, 10分
则事件B所构成的区域为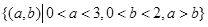
其面积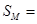
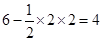 12分
12分
由几何概型的概率计算公式可得:
方程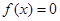 没有实根的概率
没有实根的概率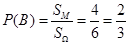 15分
15分
考点:古典概型概率与几何概型概率
点评:古典概型概率的求解主要是找到所有基本事件种数与满足题意要求的基本事件种数,然后求其比值;几何概型概率通常利用长度比,面积比体积比求解,在求解时首先要分析清楚属于哪种概率类型


科目:高中数学 来源: 题型:
| a |
| x |
| lnx |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x |
| 3 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com