
分析 (1)令x=0,可得:(1-0)5(3+2×0)9=a0(0+1)14+a1(0+1)13+…+a13(0+1)+a14,化简即可得出.
(2)令x=-2可得:a0-a1-…-a14=-35.又a0+a1+…+a14=39.即可得出.
解答 解:(1)令x=0,可得:(1-0)5(3+2×0)9=a0(0+1)14+a1(0+1)13+…+a13(0+1)+a14,
∴a0+a1+…+a14=39.
(2)令x=-2可得:(1+2)5(3-4)9=a0(-2+1)14+a1(-2+1)13+…+a13(-2+1)+a14,
∴a0-a1-…-a14=-35.
又a0+a1+…+a14=39.
∴2(a1+a3+…a13)=39+35,
∴a1+a3+…a13=38+34.
点评 本题考查了二项式定理的应用,考查了推理能力与计算能力,属于中档题.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
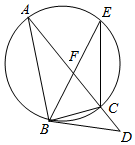 如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D
如图,△ABC为圆的内接三角形,∠ABC的平分线BF交圆于点E,过点B作圆的切线交AC的延长线于点D查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∧(¬q) | C. | (¬p)∧q | D. | p∨q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | cosθ-sinθ | B. | sinθ-cosθ | C. | $\sqrt{2}$sinθ | D. | $\sqrt{2}$cosθ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com