
分析 (Ⅰ)利用线段长度相等,建立三角方程,即可求tanα=1,利用同角三角函数基本关系式化简所求即可计算求值得解.
(Ⅱ)利用|CD|2=$\frac{5}{3}$,求出sinα+cosα=$\frac{2}{3}$,从而可得sinαcosα的值,利用同角三角函数基本关系式化简所求即可.
解答 解:(Ⅰ)由题意,∵|AC|=|BC|,
∴|AC|2=|BC|2,即(sinα-3)2+cos2α=sin2α+(cosα-3)2…(2分)
化简得sinα=cosα,
∴tanα=1,…(4分)
∵tanα=1,
∴$\begin{array}{l}\frac{4sinα-2cosα}{5cosα+3sinα}=\frac{4tanα-2}{5+3tanα}…(5分)\\=\frac{2}{8}=\frac{1}{4}…(6分)\end{array}$
(Ⅱ)由|CD|2=$\frac{5}{3}$,得:(sinα-1)2+(cosα-1)2=$\frac{5}{3}$,
化简得:sinα+cosα=$\frac{2}{3}$,…(8分)
于是:sinαcosα=$\frac{1}{2}$[(sinα+cosα)2-1]=-$\frac{5}{18}$.…(10分)
$\begin{array}{l}∴\frac{{{{sin}^2}α+sinαcosα}}{1+tanα}=\frac{sinα(sinα+cosα)}{{\frac{cosα+sinα}{cosα}}}\\=sinαcosα…(11分)\\=-\frac{5}{18}…(12分)\end{array}$
点评 本题主要考查向量的基本运算以及向量和三角函数的综合运算,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 192 | B. | 448 | C. | -192 | D. | -448 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
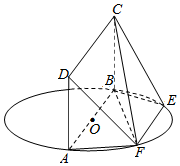 如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在平面和圆O所在的平面互相垂直.已知AB=2,EF=1.
如图,AB为圆O的直径,点E、F在圆O上,AB∥EF,矩形ABCD所在平面和圆O所在的平面互相垂直.已知AB=2,EF=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com