
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 根据向量的数量积的运算,先求出$\overrightarrow{CB}$与$\overrightarrow{AC}$的夹角为θ,再根据余弦定理即可求出答案.
解答 解:设$\overrightarrow{CB}$=$\vec a$,$\overrightarrow{AC}$=$\vec b$,设$\overrightarrow{CB}$与$\overrightarrow{AC}$的夹角为θ,
∵|$\vec a$|=2,|$\vec b$|=1,$\vec a$•$\vec b$=-1,
∴$\vec a$•$\vec b$=|$\vec a$|•|$\vec b$|cosθ=2×1×cosθ=-1,
∴cosθ=$\frac{1}{2}$,
∴θ=120°,
∴∠ACB=60°,
由余弦定理可得|$\overrightarrow{AB}$|2=|$\vec a$|2+|$\vec b$|2-2|$\vec a$|•|$\vec b$|cos60°=4+1-2×2×1×$\frac{1}{2}$=3,
∴|$\overrightarrow{AB}$|=$\sqrt{3}$,
故选:C.
点评 本题考查了向量的数量积的运算和余弦定理,考查运算能力,属于中档题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 8 | C. | 7 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{10}{9}$ | B. | 4 | C. | $\frac{40}{9}$ | D. | $\frac{56}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
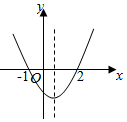 函数f(x)=$\frac{1}{3}$x3+ax2+bx+c(a,b,c∈R)的导函数的图象如图所示:
函数f(x)=$\frac{1}{3}$x3+ax2+bx+c(a,b,c∈R)的导函数的图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)与g(x)的最大值不同 | |
| B. | 函数f(x)与g(x)在$(\frac{3π}{4},\;\;\frac{5π}{4})$上都为增函数 | |
| C. | 函数f(x)与g(x)的图象的对称轴相同 | |
| D. | 将函数f(x)的图象上各点的横坐标缩短为原来的$\frac{1}{2}$,纵坐标不变,再通过平移能得到g(x)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{5}{9}$ | C. | 1 | D. | -3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com