【题目】如图，在四棱锥
中，
面
，
，
，
，
，
是
的中点.
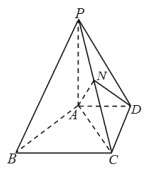
（1）求证：
平面
；
（2）求三棱锥
的体积.
【答案】(1)详见解析;(2) 
.
【解析】
试题（1）取
中点
连结
. ，推导出四边形
是平行四边形，从而
由此能证明
平面
．
（2）
到面
的距离等于
到面的距离的一半，且
，从而三棱锥
的高是2，由此能求出三棱锥的体积．
试题解析：(1)如图，取PB中点M，连结AM，MN.
∵MN是△BCP的中位线,∴MN∥
BC，且MN=BC.
依题意得,AD
BC,则有AD
MN
∴四边形AMND是平行四边形,∴ND∥AM
∵ND面PAB，AM面PAB，
∴ND∥面PAB
(2)∵N是PC的中点，
∴N到面ABCD的距离等于P到面ABCD的距离的一半，且PA⊥面ABCD，PA=4，
∴三棱锥NACD的高是2.
在等腰△ABC中,AC=AB=3,BC=4,BC边上的高为
.
BC∥AD,∴C到AD的距离为
，
∴S△ADC=
.
∴三棱锥NACD的体积是
.
科目：高中数学 来源： 题型：
【题目】某大城市一家餐饮企业为了了解外卖情况，统计了某个送外卖小哥某天从9:00到21:00这个时间段送的50单外卖.以2小时为一时间段将时间分成六段，各时间段内外卖小哥平均每单的收入情况如下表，各时间段内送外卖的单数的频率分布直方图如下图.
时间区间 |
|
|
|
|
|
|
每单收入（元） | 6 | 5.5 | 6 | 6.4 | 5.5 | 6.5 |
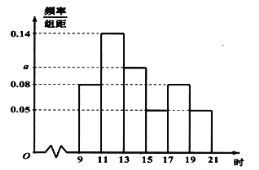
（Ⅰ）求频率分布直方图中
的值，并求这个外卖小哥送这50单获得的收入；
（Ⅱ）在这个外卖小哥送出的50单外卖中男性订了25单，且男性订的外卖中有20单带饮品，女性订的外卖中有10单带饮品，请完成下面的
列联表，并回答是否有
的把握认为“带饮品和男女性别有关”？
带饮品 | 不带饮品 | 总计 | |
男 | |||
女 | |||
总计 |
附：
| 0.050 | 0.010 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平行四边形
中，
，
，过
点作
的垂线，交的延长线于点
，
.连结
，交
于点
，如图1，将
沿折起，使得点到达点
的位置，如图2.
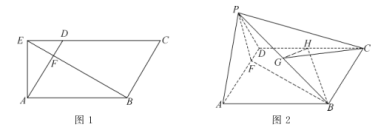
（1）证明：平面
平面
；
（2）若
为
的中点，
为的中点，且平面
平面，求三棱锥
的体积.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，D为正三棱柱ABC﹣A1B1C1的棱AC的中点．
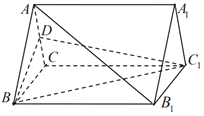
（1）证明：AB1∥平面BC1D
（2）若二面角C﹣BC1﹣D的大小为45°，求直线AB与平面BB1C1C夹角的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，以
为极点，
轴的正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
；直线
的参数方程为
（
为参数），直线与曲线分别交于
，
两点.
（1）写出曲线的直角坐标方程和直线的普通方程；
（2）若点
的极坐标为
，
，求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】奇函数f（x）在R上存在导数
，当x＜0时，
f（x），则使得（x2﹣1）f（x）＜0成立的x的取值范围为（ ）
A.（﹣1，0）∪（0，1）B.（﹣∞，﹣1）∪（0，1）
C.（﹣1，0）∪（1，+∞）D.（﹣∞，﹣1）∪（1，+∞）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市旅游管理部门为提升该市26个旅游景点的服务质量，对该市26个旅游景点的交通、安全、环保、卫生、管理五项指标进行评分．每项评分最低分0分，最高分100分．每个景点总分为这五项得分之和，根据考核评分结果，绘制交通得分与安全得分散点图、交通得分与景点总分散点图如图
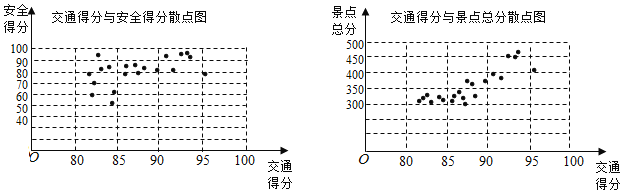
请根据图中所提供的信息，完成下列问题：
（1）若从交通得分排名前5名的景点中任取1个，求其安全得分大于90分的概率；
（2）若从景点总分排名前6名的景点中任取3个，记安全得分不大于90分的景点个数为ξ，求随机变量ξ的分布列和数学期望；
（3）记该市26个景点的交通平均得分为
，安全平均得分为
，写出和的大小关系？（只写出结果）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
