
矩形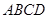 的中心在坐标原点,边
的中心在坐标原点,边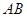 与
与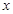 轴平行,
轴平行,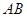 =8,
=8,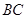 =6.
=6.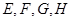 分别是矩形四条边的中点,
分别是矩形四条边的中点,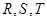 是线段
是线段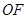 的四等分点,
的四等分点,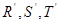 是线段
是线段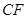 的四等分点.设直线
的四等分点.设直线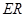 与
与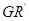 ,
,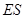 与
与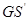 ,
,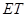 与
与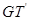 的交点依次为
的交点依次为 .
.
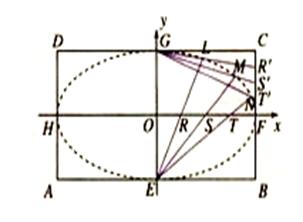
(1)以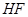 为长轴,以
为长轴,以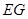 为短轴的椭圆Q的方程;
为短轴的椭圆Q的方程;
(2)根据条件可判定点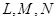 都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段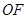 的
的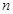 (
( 等分点从左向右依次为
等分点从左向右依次为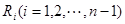 ,线段
,线段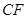 的
的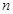 等分点从上向下依次为
等分点从上向下依次为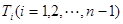 ,那么直线
,那么直线 与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
(1)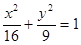 ;(2)详见解析;(3)
;(2)详见解析;(3)
【解析】
试题分析:根据长轴长 ,短轴长
,短轴长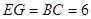 ,可求出椭圆的方程;根据点
,可求出椭圆的方程;根据点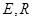 的坐标可写出直线
的坐标可写出直线 的方程,同理也可写出直线
的方程,同理也可写出直线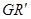 的方程,再求出它们的交点
的方程,再求出它们的交点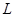 的坐标,验证
的坐标,验证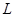 在椭圆上即可得证;类比(2)的结论,即可得到直线
在椭圆上即可得证;类比(2)的结论,即可得到直线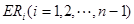 与直线
与直线 的交点一定在椭圆Q上.
的交点一定在椭圆Q上.
试题解析:
根据题意可知,椭圆的焦点在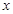 轴上,可设其标准方程为
轴上,可设其标准方程为 ,
,
因为长轴长 ,短轴长
,短轴长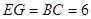 ,所以
,所以 ,
,
所以所求的椭圆的标准方程为: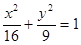 .
.
由题意知,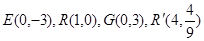
可得直线 的方程为
的方程为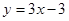 ,直线
,直线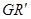 的方程为
的方程为 ,
,
联立可解得其交点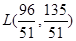 ,将
,将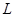 的坐标代入椭圆方程
的坐标代入椭圆方程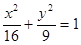 成立,即点
成立,即点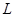 在椭圆上得证.
在椭圆上得证.
另法:设直线 、
、 交点
交点 ,
,
由 三点共线得:
三点共线得: ①
①
由 三点共线得:
三点共线得: ②
②
①②相乘,整理可得 ,即
,即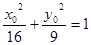

所以L在椭圆上.
(3)类比(2)的结论,即可得到直线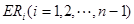 与直线
与直线 的交点一定在椭圆Q上.
的交点一定在椭圆Q上.
考点:本题考查了直线的方程,椭圆的方程的求解方法,以及直线与圆锥曲线的位置关系.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2015届安徽池州第一中学高二上学期期中考试文科数学试卷(解析版) 题型:解答题
矩形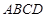 的中心在坐标原点,边
的中心在坐标原点,边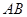 与
与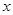 轴平行,
轴平行,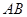 =8,
=8,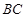 =6.
=6.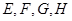 分别是矩形四条边的中点,
分别是矩形四条边的中点,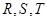 是线段
是线段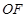 的四等分点,
的四等分点,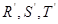 是线段
是线段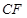 的四等分点.设直线
的四等分点.设直线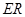 与
与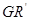 ,
,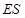 与
与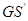 ,
,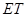 与
与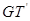 的交点依次为
的交点依次为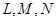 .
.
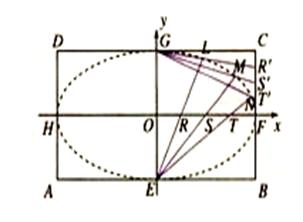
(1)求以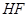 为长轴,以
为长轴,以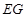 为短轴的椭圆Q的方程;
为短轴的椭圆Q的方程;
(2)根据条件可判定点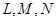 都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
都在(1)中的椭圆Q上,请以点L为例,给出证明(即证明点L在椭圆Q上).
(3)设线段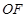 的
的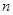 (
(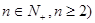 等分点从左向右依次为
等分点从左向右依次为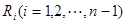 ,线段
,线段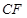 的
的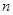 等分点从上向下依次为
等分点从上向下依次为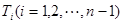 ,那么直线
,那么直线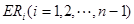 与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
与哪条直线的交点一定在椭圆Q上?(写出结果即可,此问不要求证明)
查看答案和解析>>
科目:高中数学 来源:2014届河南灵宝第三高级中学高二上学期第三次质量检测理数学(解析版) 题型:解答题
(本小题满分12分)已知椭圆的中心在坐标原点O,长轴长为2 ,离心率e=
,离心率e=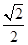 ,过右焦点F的直线l交椭圆于P、Q两点.
,过右焦点F的直线l交椭圆于P、Q两点.
(Ⅰ)求椭圆的方程;
(Ⅱ)若OP、OQ为邻边的平行四边形是矩形,求满足该条件的直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com