练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
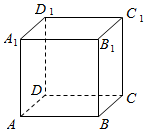
    12．正方体ABCD-A1B1C1D1中，E为A1A的三等分点，F为C1C的三等分点，AE=2A1E，CF=2C1F，过B，E，F作正方体的截面，画出截面在面ACC1A1上的正投影图．

    分析 取D1D的三等分点G，DG=2D1G，再取GD1的三等分点H，GH=2D1H，则平面BEHF是过B，E，F所作的正方体的截面，由此能作出截面BEHF在面ACC1A1上的正投影图．

    解答 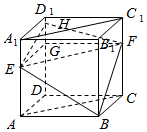解：∵正方体ABCD-A1B1C1D1中，E为A1A的三等分点，F为C1C的三等分点，AE=2A1E，CF=2C1F，
    取D1D的三等分点G，DG=2D1G，再取GD1的三等分点H，GH=2D1H，
    连结EH，FH，则平面BEHF是过B，E，F所作的正方体的截面，如右图．
    ∴截面BEHF在面ACC1A1上的正投影图为：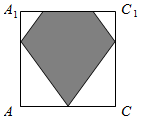

    点评 本题考查截面的作法及截面的正投影图的画法，是基础题，解题时要认真审题，注意空间思维能力的培养．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．已知点F（0，1）为抛物线x2=2py的焦点．
    （1）求抛物线C的方程；
    （2）点A、B、C是抛物线上三点且$\overrightarrow{FA}$+$\overrightarrow{FB}$+$\overrightarrow{FC}$=$\overrightarrow{0}$，求△ABC面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．若数列{an}的前n项和为Sn，且对任意正整数n都有2an-Sn=4．
    （1）求数列{an}的通项公式；
    （2）令bn=（-1）n•$\frac{2n+3}{{{log}_{2}a}_{n}{{•log}_{2}a}_{n+1}}$，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．如图，将直角梯形ABCD绕AB所在的直线旋转一周，由此形成的几何体是由哪些基本几何体构成的？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．若x、y∈R，且（x-1）+yi＞2x，求x，y的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知实数x，y满足不等式$\left\{\begin{array}{l}{2x-y≥0}\\{x+y-4≥0}\\{x≤2}\end{array}\right.$，则$\frac{2{x}^{2}-{y}^{2}}{{x}^{2}+{y}^{2}}$的取值范围是[-$\frac{2}{5}$，1]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．已知数列{an}的前n项和Sn=m•qn+n（m，n，q为非零常数），求证：{an}为等比数列?m+n=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=sin（ωx+φ）（|φ|＜$\frac{π}{2}$）的图象在y轴上的截距为$\frac{\sqrt{3}}{2}$，点P（x1，y1），Q（x2，y2）是函数f（x）图上的任意两点，当|y1-y2|=2时，|x1-x2|的最小值为2π．
    （Ⅰ）求函数f（x）的解析式；
    （Ⅱ）要得到函数y=sinx的图象，可以将函数y=f（x）的图象作怎样的变换？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．某工程队要装修一住宅小区的一批新房，若装修一栋别墅，木工需360小时，瓦工需240小时；若装修一套公寓房，木工需180小时，瓦工需300小时．工程队有18000个木工工时和15600个瓦工工时可以使用．若装修一栋别墅利润为4万元，装修一套公寓房利润为3万元，要制定怎样的装修计划，能使工程队得到的最多的利润？

    查看答案和解析>>

    同步练习册答案