
分析 (1)利用递推关系、等比数列的通项公式即可得出;
(2)利用“裂项求和”、分类讨论方法即可得出.
解答 解:(1)∵对任意正整数n都有2an-Sn=4,
∴2a1-a1=4,解得a1=4;
当n≥2时,2an-1-Sn-1=4,可得:2an-2an-1-an=0,化为an=2an-1,
∴数列{an}是等比数列,首项为4,公比为2,
∴an=4×2n-1=2n+1.
(2)bn=(-1)n•$\frac{2n+3}{{{log}_{2}a}_{n}{{•log}_{2}a}_{n+1}}$=(-1)n$•\frac{2n+3}{(n+1)(n+2)}$=(-1)n$(\frac{1}{n+1}+\frac{1}{n+2})$,
∴当n=2k(k∈N*)时,数列{bn}的前n项和Tn=T2k=$-(\frac{1}{2}+\frac{1}{3})$+$(\frac{1}{3}+\frac{1}{4})$-…+$(\frac{1}{n+1}+\frac{1}{n+2})$=-$\frac{1}{2}+\frac{1}{n+2}$=$\frac{-n}{2n+4}$.
当n=2k-1(k∈N*)时,数列{bn}的前n项和Tn=T2k-1=$-(\frac{1}{2}+\frac{1}{3})$+$(\frac{1}{3}+\frac{1}{4})$-…-$(\frac{1}{n+1}+\frac{1}{n+2})$=-$\frac{1}{2}$-$\frac{1}{n+2}$=-$\frac{n+4}{2n+4}$.
∴Tn=$\left\{\begin{array}{l}{\frac{-n}{2n+4},n为偶数}\\{-\frac{n+4}{2n+4},n为奇数}\end{array}\right.$.
点评 本题考查了递推关系、等比数列的通项公式、“裂项求和”方法、对数的运算性质,考查了分类讨论方法、推理能力与计算能力,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:解答题
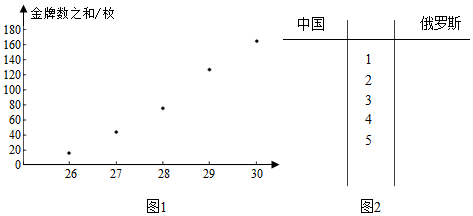
| 第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
| 中国 | 38 | 51 | 32 | 28 | 16 |
| 俄罗斯 | 24 | 23 | 27 | 32 | 26 |
| 时间x(届) | 26 | 27 | 28 | 29 | 30 |
| 金牌数之和y(枚) | 16 | 44 | 76 | 127 | 165 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 7 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,在平面直角坐标系xOy中,点A在x轴正半轴上,直线AB的倾斜角为$\frac{3π}{4}$,OB=4,设∠AOB=θ,θ∈($\frac{π}{2}$,$\frac{3π}{4}$).
如图所示,在平面直角坐标系xOy中,点A在x轴正半轴上,直线AB的倾斜角为$\frac{3π}{4}$,OB=4,设∠AOB=θ,θ∈($\frac{π}{2}$,$\frac{3π}{4}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
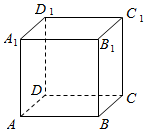 正方体ABCD-A1B1C1D1中,E为A1A的三等分点,F为C1C的三等分点,AE=2A1E,CF=2C1F,过B,E,F作正方体的截面,画出截面在面ACC1A1上的正投影图.
正方体ABCD-A1B1C1D1中,E为A1A的三等分点,F为C1C的三等分点,AE=2A1E,CF=2C1F,过B,E,F作正方体的截面,画出截面在面ACC1A1上的正投影图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com